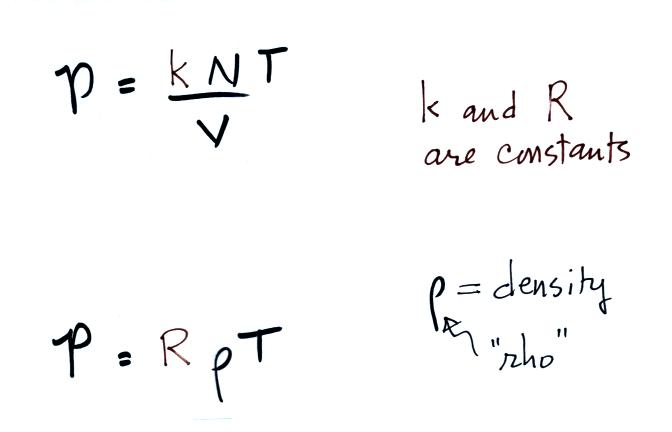Thursday Feb. 5, 2015
Adele (live at the Royal Albert Concert Hall): "I'll be Waiting"
(3:44), "If it
Hadn't Been for Love" (5:20), "One and Only"
(5:52), "Turning
Tables" (4:04)
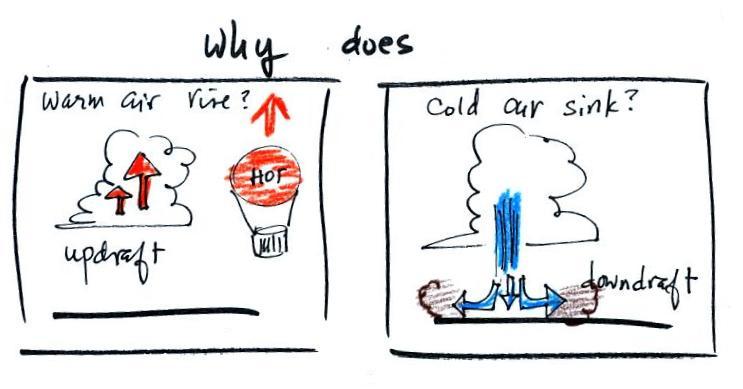
Warm air rises & cold air sinks
Our objective today in the time leading up to Practice Quiz will
be to become acquainted with the ideal gas law. That is the
1st step in trying to understand why warm air rises and cold air
sinks (the figure below is found at the top of p. 49 in the
ClassNotes). It's also something that students
working on Experiment #1 might want to mention in their reports.
Hot air balloons rise, so does the relatively warm air in a
thunderstorm updraft (it's warmer than the air around
it). Conversely cold air sinks. The surface
winds caused by a thunderstorm downdraft (as shown above) can
reach speeds of 100 MPH (stronger than most tornadoes) and are a
serious weather hazard that we'll come back to later in the
semester.
A full understanding of these rising and sinking motions is a
3-step process (the following is from the bottom part of p. 49
in the photocopied ClassNotes). We'll only get
to Step #1 today.
Ideal gas law - air pressure on a microscopic scale
The ideal gas law is an equation that tells you which properties
of the air inside a balloon work to determine the air's
pressure.
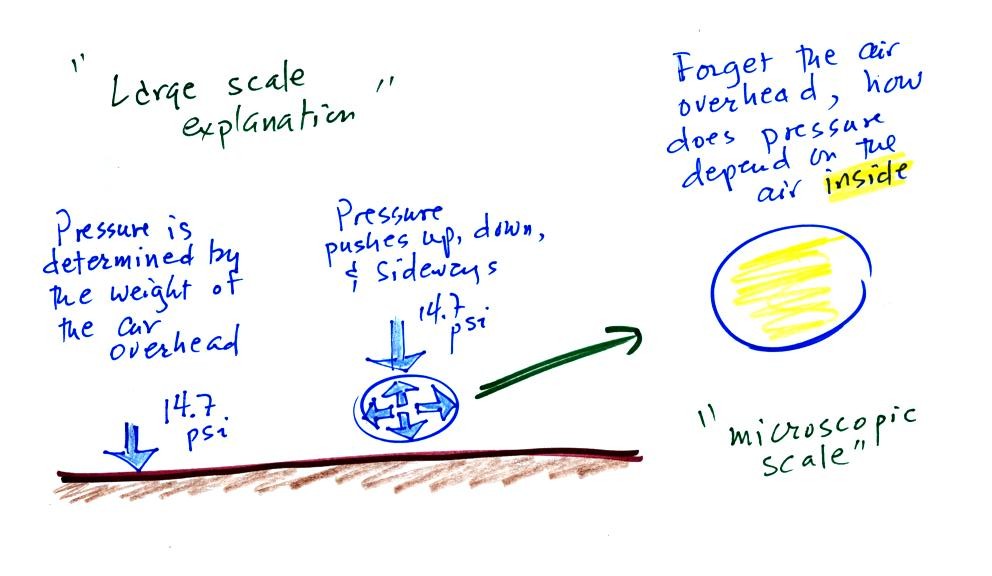
We then went a bit further and tried to imagine the weight of
the atmosphere pushing down on a balloon sitting on the
ground. If you actually do push on a balloon you realize
that the air in the balloon pushes back with the same
force. Air everywhere in the atmosphere pushes upwards,
downwards, and sideways.
These are large scale, atmosphere size, ways of thinking about
pressure. Next we are going to concentrate on just the
air in the balloon pictured above. This is more of a
microscopic view of pressure.
Imagine filling a balloon with air. If you could
look inside which picture below would be more realistic?
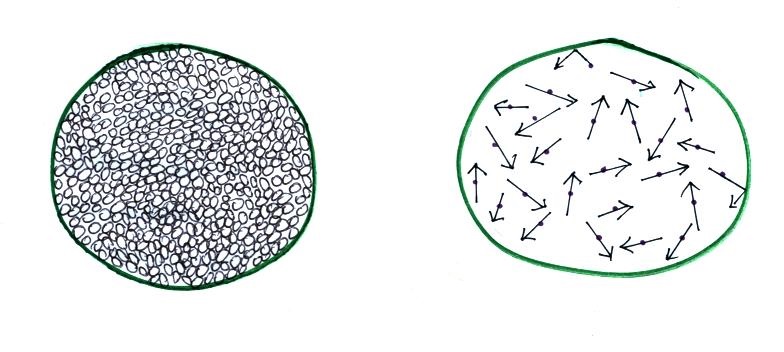
The view on the left is incorrect.
The air molecules actually do not fill the balloon and
take up all the available space.
|
This is the correct
representation.
The air molecules are moving
around at 100s of MPH but actually take up little or
no space in the balloon.
|
The air molecules are continually colliding
with the walls of the balloon and pushing outward (this force
divided by area is the pressure). Wikipedia
has a
nice animation. An individual molecule doesn't exert
a very strong force, but there are so many molecules that the
combined effect is significant.
What do you need to know about the air inside the balloon to be
able to determine the pressure it produces?
We want to identify the properties or characteristics of the
air inside the balloon that determine the pressure and then put
them together into an equation called the ideal gas law.
Variables in the ideal gas law &
how they affect pressure
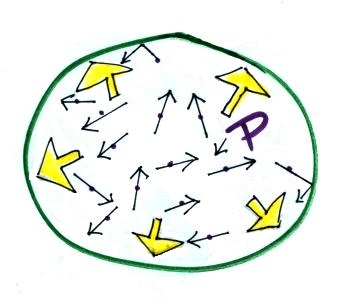
In A
the pressure produced by the air molecules inside a
balloon will first depend on how many air molecules are there,
N. If there weren't any air molecules at all there
wouldn't be any pressure.
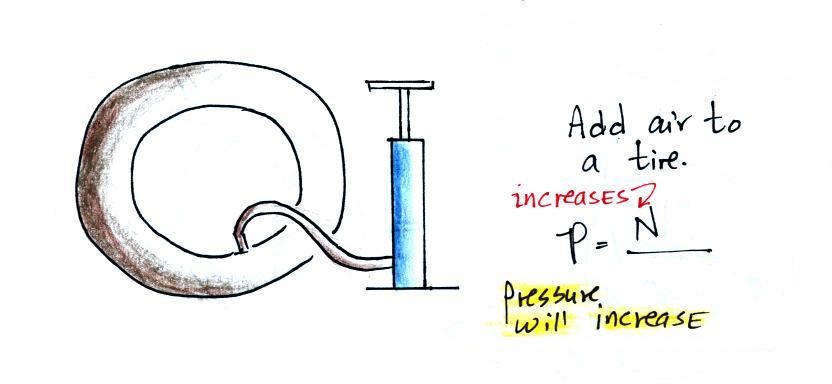
Here's an example. You're adding
air to a tire. As you add more and more air to something
like a bicycle tire, the pressure increases. Pressure is directly
proportional to N; an increase in N causes an increase in
P. If N doubles, P also doubles (as long as the other
variables in the equation don't change).
In B
air pressure inside a balloon also
depends on the size of the balloon. If you try to
compress and balloon and reduce its volume the air
pressure increases and "fights back." A decrease
in volume causes an increase in pressure, that's an
inverse proportionality.
Note
it is possible to keep pressure
constant by changing N and V together in just the right
kind of way. This is what happens in Experiment #1
that some students are working on. Here's a little
more detailed look at that experiment.
|
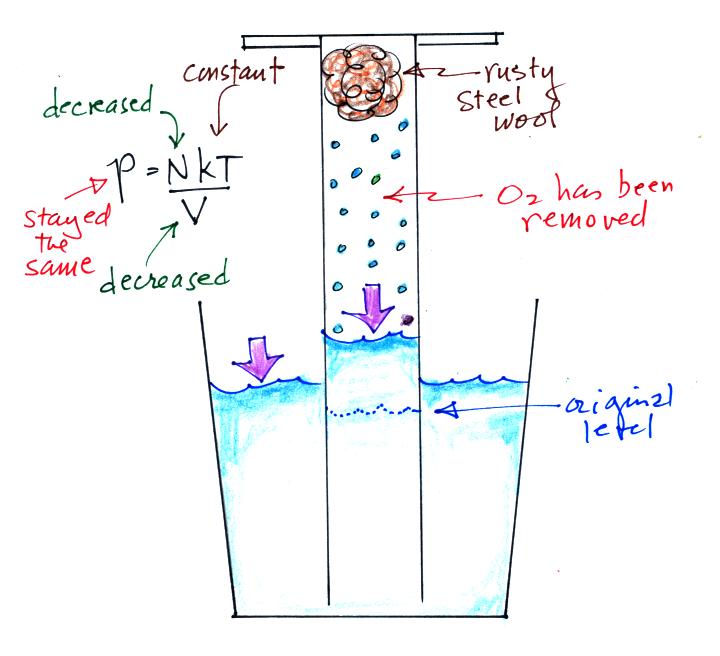
|
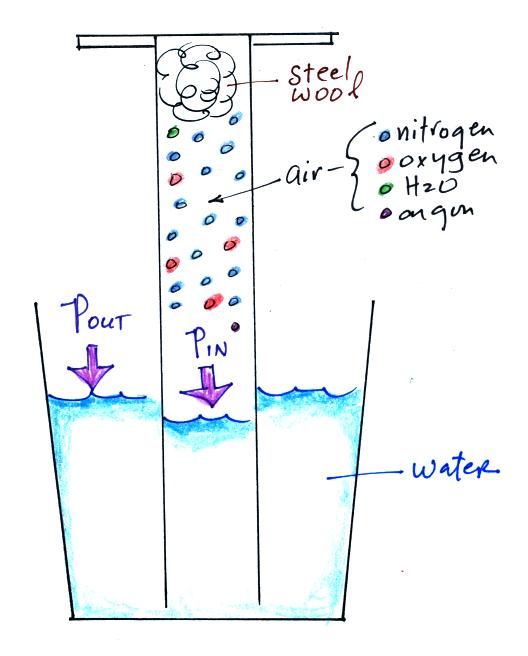
An
air sample is trapped together with some steel wool
inside a graduated cylinder. The cylinder is
turned upside down and the open end is stuck into a
glass of water sealing off the air sample from the rest
of the atmosphere. This is shown at left
above. The pressure of air outside the cylinder
tries to push water into the cylinder, the pressure of
the air inside keeps the water out.
Oxygen in the cylinder reacts with
steel wool to form rust. Oxygen is removed from
the air sample which causes N (the total number of air
molecules) to decrease. Removal of oxygen would
ordinarily cause a drop in Pin
and
upsets the balance between Pin
and Pout
. But, as oxygen
is removed, water rises up into the cylinder decreasing
the air sample volume. The decrease in V causes Pin
to increase. What actually happens is that N and V
both decrease together in the same relative amounts and
the air sample pressure remains constant.
If you were to remove 20% of the air molecules, V would
decrease to 20% of its original value and pressure would stay
constant. It is the change in V that you can measure and
use to determine the oxygen percentage concentration in air.
Part
C: Increasing the temperature of the gas in a
balloon will cause the gas molecules to move more
quickly (kind of like "Mexican
jumping beans"). They'll collide with the
walls of the balloon more frequently and rebound with
greater force. Both will increase the pressure.
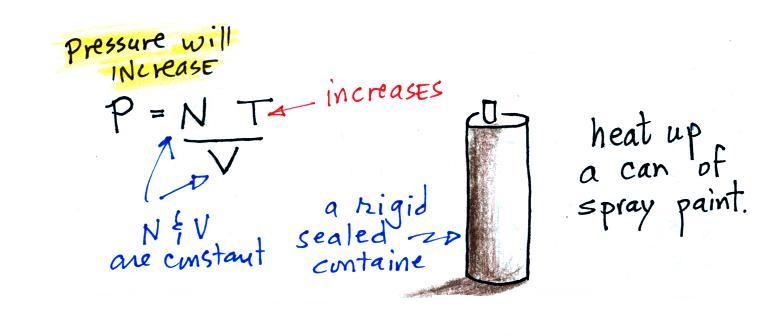
You shouldn't throw
a can of spray paint into a fire because the
temperature will cause the pressure inside the can to
increase and the can could explode.
Surprisingly, as explained in Part D, the pressure does
not depend on the mass of the molecules. Pressure
doesn't depend on the composition of the gas. Gas
molecules with a lot of mass will move slowly, the less
massive molecules will move more quickly. The massive
slow moving molecules collide with the walls of the container
with the same force as the smaller ones.
The figure below (which replaces the bottom of p. 51 in the
photocopied ClassNotes) shows two forms of the ideal gas
law. The top equation is the one we just "derived" and
the bottom is a second slightly different version. You
can ignore the constants k and R if you are just trying to
understand how a change in one of the variables would affect
the pressure. You only need the constants when you are
doing a calculation involving numbers and units (which we
won't be doing).
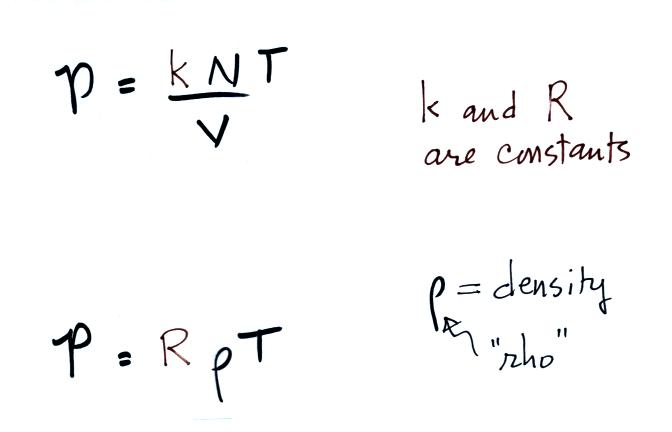
The ratio N/V is similar to density
(mass/volume). That's where the ρ (density)
term in the second equation comes from.
This left more than enough time
for the Practice Quiz.
If you weren't in class to take the Practice Quiz you can download a copy here.
Then you can check your answers against those found here.