Wed., Sept. 5, 2012
click here to download today's notes in a more printer friendly format

Time for 3 songs from Crooked Still before class this afternoon ("Foggy Mountain Special", "American Tune", and "Baby, What's Wrong With You?")

The first of the Optional Assignments is now online.  You don't have to do these assignments, but if you do you can earn extra credit.  I'll hand out copies of the assignment in class on Friday, the assignment is due at the beginning of class on Fri., Sep. 14.  You should have the assignment done before coming to class.

Also the report writing guidelines for the 1S1P Discovery of Oxygen topic have finally be completed.  The 1S1P reports are due next Monday, Sept. 10.

We spent about the first 20 minutes of class covering some new material.  If there were a real quiz today (rather than a Practice Quiz) you would have been given the full period for the quiz.

If you weren't in class you can download a copy of the Practice Quiz.  I would suggest you do that so that you can see what the quizzes look like.  Answers will become available sometime on Thursday (Sep. 6)

You can learn a lot about pressure from bricks. 

For example the photo below (taken in my messy office) shows two of the bricks from class.  One is sitting flat, the other is sitting on its end.  Each brick weighs about 5 pounds.  Would the pressure at the base of each brick be the same or different in this kind of situation? 



Pressure is determined by (depends on) weight so you might think the pressures would be equal.  But pressure is weight divided by area.  In this case the weights are the same but the areas are different.  In the situation at left the 5 pounds must be divided by an area of about 4 inches by 8 inches = 32 inches.  That works out to be about 0.15 psi.  In the other case the 5 pounds should be divided by a smaller area, 4 inches by 2 inches = 8 inches.  That's a pressure of 0.6 psi, 4 times higher.  Notice also these pressures are much less the 14.7 psi sea level atmospheric pressure.

The main reason I brought the bricks was so that you could understand what happens to pressure with increasing altitude.  Here's a drawing of the 5 bricks stacked on top of each other.

At the bottom of the pile you would measure a weight of 25 pounds (if you wanted to find the pressure you'd divide 25 lbs by the 32 square inch area on the bottom of the brick).  If you moved up a brick you would measure a weight of 20 pounds, the weight of the four bricks that are still above.  The pressure would be less.  Weight and pressure will decrease as you move up the pile.

The atmosphere is really no different.  Pressure at any level is determined by the weight of the air still overhead.  Pressure decreases with increasing altitude because there is less and less air remaining overhead. 



At sea level altitude, at Point 1, the pressure is normally about 1000 mb.  That is determined by the weight of all (100%) of the air in the atmosphere.

Some parts of Tucson, at Point 2, are 3000 feet above sea level (most of central Tucson is a little lower than that around 2500 feet).  At 3000 ft. about 10% of the air is below, 90% is still overhead.  It is the weight of the 90% that is still above that determines the atmospheric pressure in Tucson.  If 100% of the atmosphere produces a pressure of 1000 mb, then 90% will produce a pressure of 900 mb. 

Pressure is typically about 700 mb at the summit of Mt. Lemmon (9000 ft. altitude at Point 3) and 70% of the atmosphere is overhead..

Pressure decreases rapidly with increasing altitude.  We will find that pressure changes more slowly if you move horizontally.  Pressure changes about 1 mb for every 10 meters of elevation change.  Pressure changes much more slowly normally if you move horizontally: about 1 mb in 100 km.  Still the small horizontal changes are what cause the wind to blow and what cause storms to form.

Point 4 shows a submarine at a depth of about 30 ft. or so.  The pressure there is determined by the weight of the air and the weight of the water overhead.  Water is much denser and much heavier than air.  At 30 ft., the pressure is already twice what it would be at the surface of the ocean (2000 mb instead of 1000 mb).

This next figure explains the rate of pressure change as you move or down in the atmosphere depends on air density.  In particular air pressure will decrease more quickly when you move upward through high density air than if you move upward through low density air.


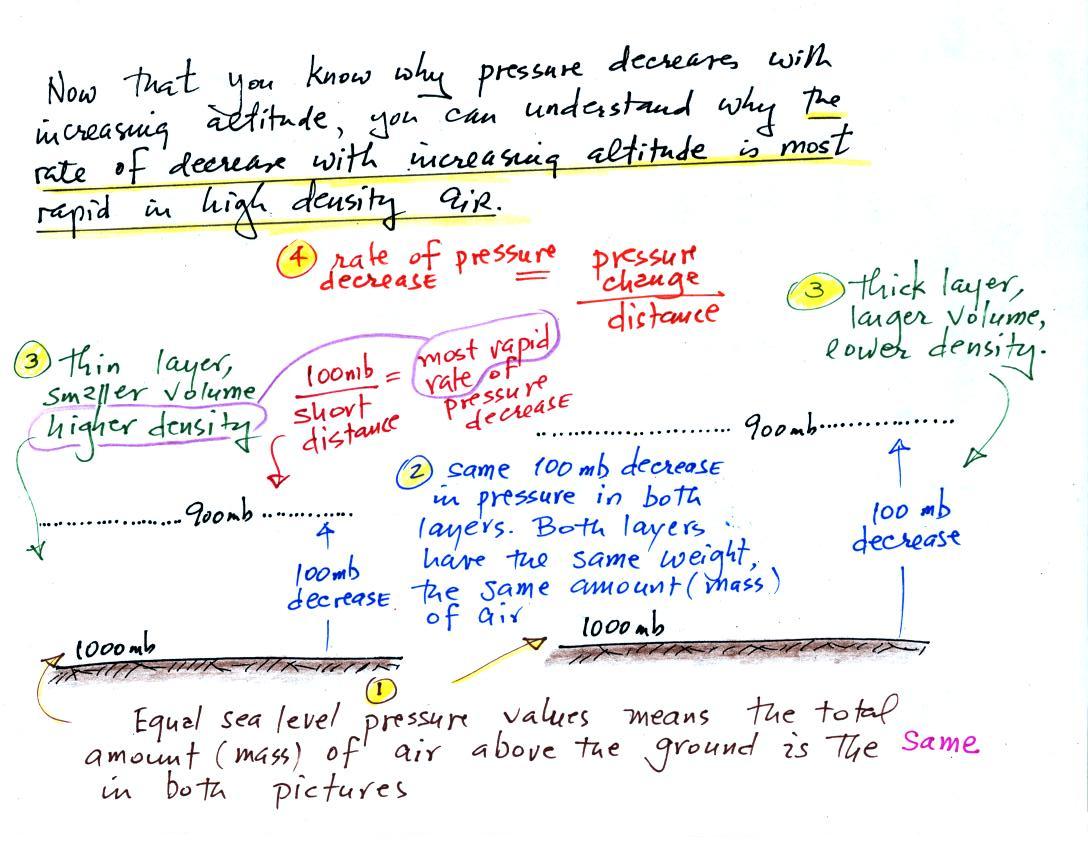
There's a lot going on in this picture, we'll examine it step by step.

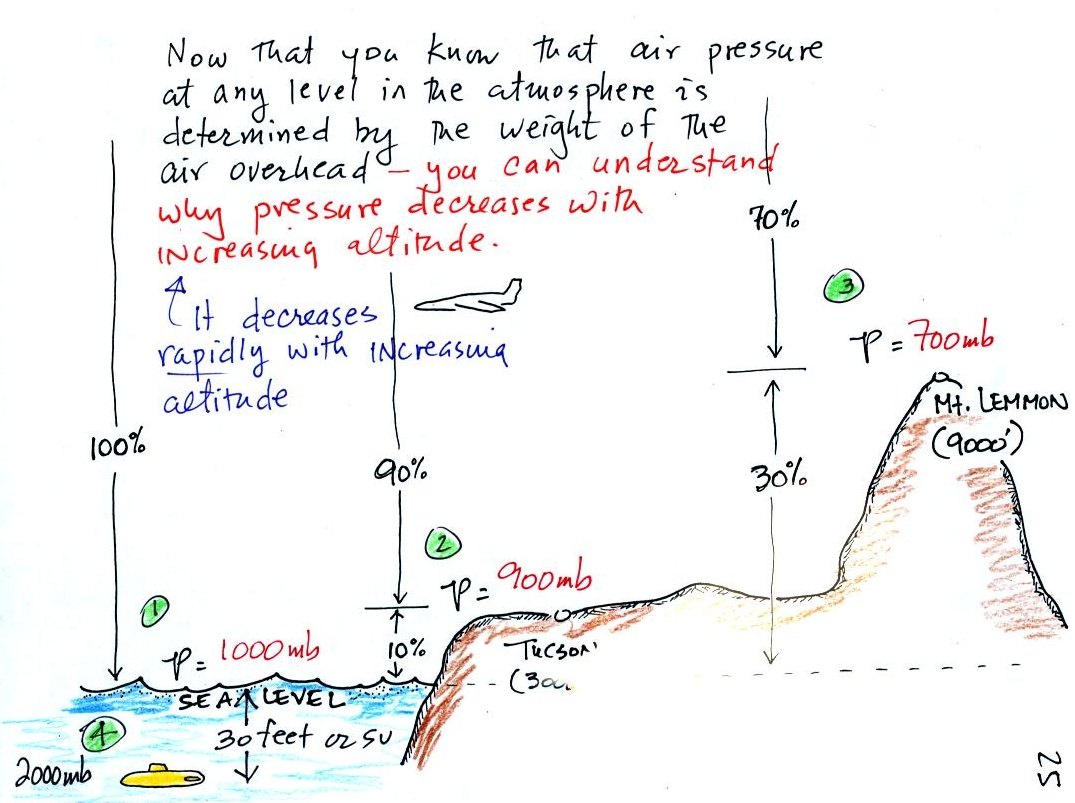
1.The sea level pressure is the same, 1000 mb, in both pictures.  Since pressure is determined by the weight of the air overhead, the weight of the air overhead in the left picture is the same as in the right picture.  The amount (mass) of air above sea level in both pictures is the same.

2.  There is a 100 mb drop in pressure in both air layers.  Pressure has decreased because air that was overhead (the air between the ground the level of the dotted line) is now underneath.  Because the pressure change is the same in both pictures the weight of the air layers are the same.  The thin layer at left has the same weight as the thicker layer at right.  Both layers contain the same amount (mass) of air.

3.  Both layers contain the same amount (mass) of air.  The air in the layer at left is thinner.  The air is squeezed into a smaller volume.  The air in the layer at left is denser than the air in the layer at right.

4.  To determine the rate of pressure decrease you divide the pressure change (100 mb for both layers) by the distance over which that change occurs.  The 100 mb change takes place in a shorter distance in the layer at left than in the layer at right.  The left layer has the highest rate of pressure decrease with increasing altitude.

So both the most rapid rate of pressure decrease with altitude and the densest air are found in Layer A.

The fact that the rate of pressure decrease with increasing altitude depends on air density is a fairly subtle but important concept.  This concept will come up 2 or 3 more times later in the semester.  For example, we will need this concept to explain why hurricanes can intensify and get as strong as they do.