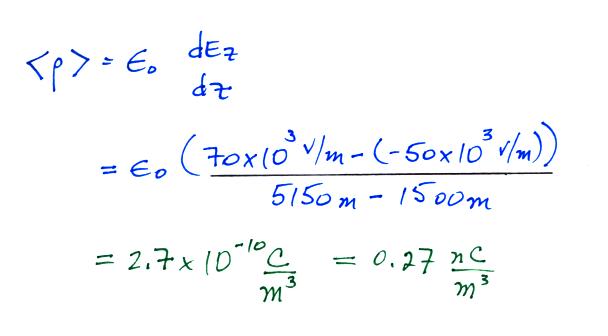Monday Feb. 2, 2015
The following handout gives a rough, back-of-the-envelope
kind of estimate of the factor of enhancement.
This might require a little
explanation.
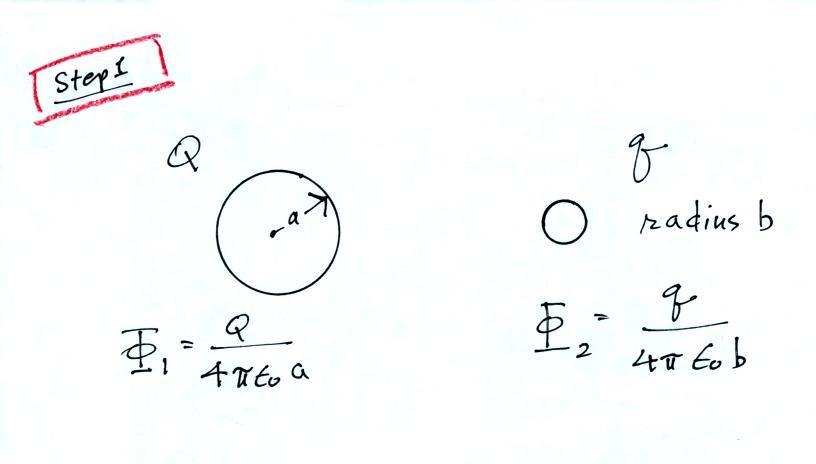
First you write down the
potential at the surface of two conducting spheres of radius a
and b, carrying charges Q and q (really just the potential a
distance a or b from a point charge Q or q)
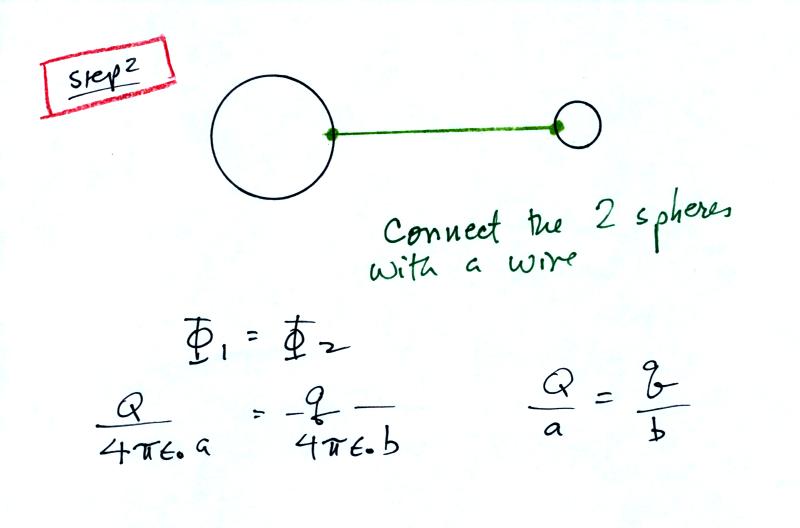
Then you connect the two spheres
with a wire which forces the two potentials to be equal (this
would of course cause the charge to rearrange themselves and
turn this into a much more complex problem, but we will ignore
that).
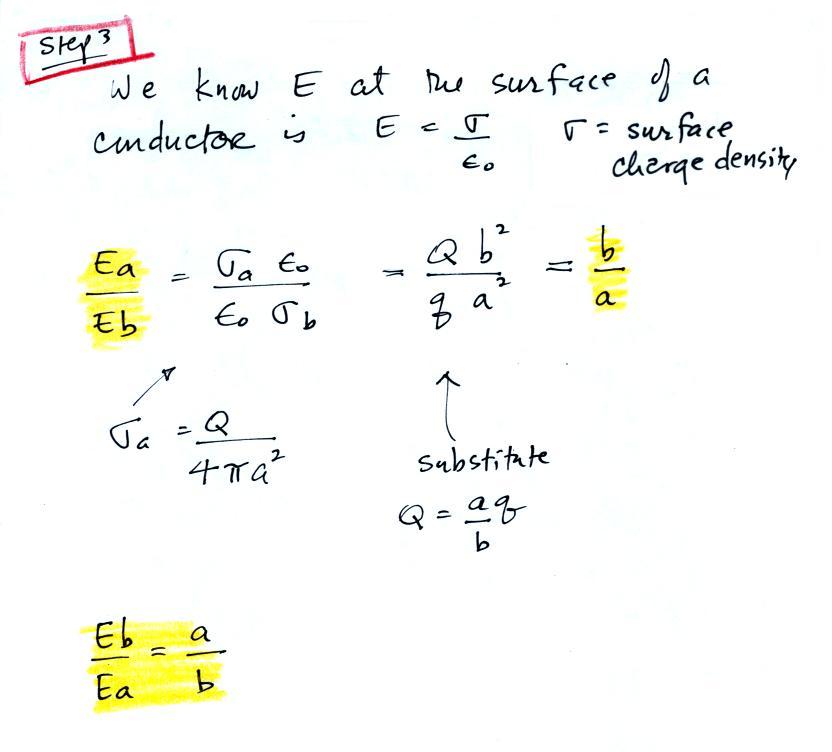
Finally we write down
expressions for the relative strengths of the electric fields at
the surfaces of the two spheres (we assume Q and q would be
uniformly spread out over the two spheres which wouldn't be
true). We see that the field at the surface of the smaller
sphere is a/b times larger than the field at the surface of the
bigger sphere.
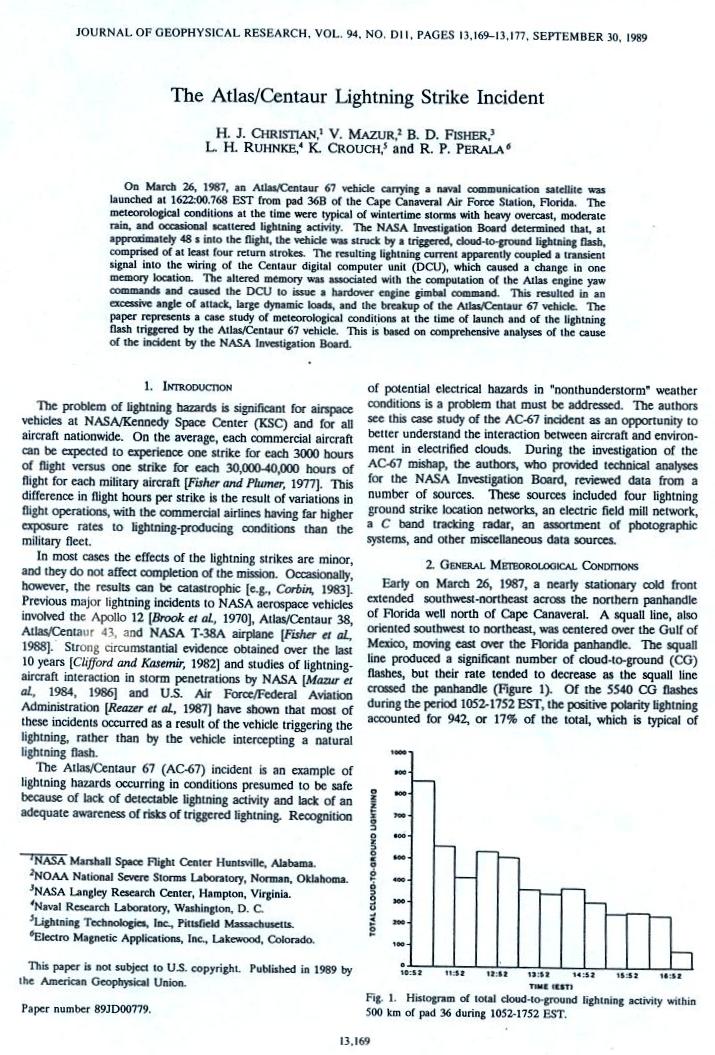
Here is a real example of field enhancement
that lead to triggering of a lightning strike and subsequent
loss of a launch vehicle (you'll find the entire article here)
In this case the rocket body together with
the exhaust plume created a long pointed conducting
object. Enhanced fields at the top and bottom triggered
lightning.

Lightning also strikes aircraft. Here's an
example. Often the discharge is initiated by the
airplane.
We'll talk about triggered lightning later in the course.
I'm referring to lightning that is purposely trigger so that it
can strike instrumentation on the ground and studied at close
range.
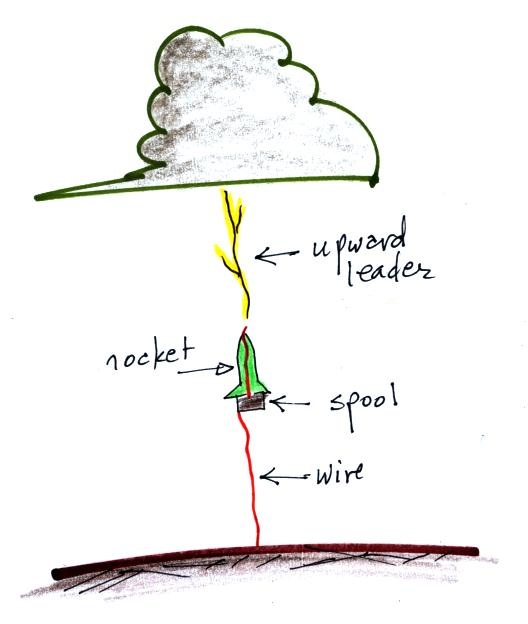
The basic idea is to launch a small rocket (about 3 feet
tall) in a high electric field under a thunderstorm. A
spool of wire is mounted on the tail fins of the rocket.
One end of the wire is connected to ground and the other end
runs up to the nose of the rocket. Wire un-spools
(probably the hardest part is to keep the wire from breaking)
once the rocket is launched forming a narrow tall conducting
object. Field enhancement at the top of the rocket is
enough often times to initiate an upward leader discharge that
then triggers lightning.
An example
from the ICLRT (International Center for Lightning Research and
Testing) operated by the University of Florida.
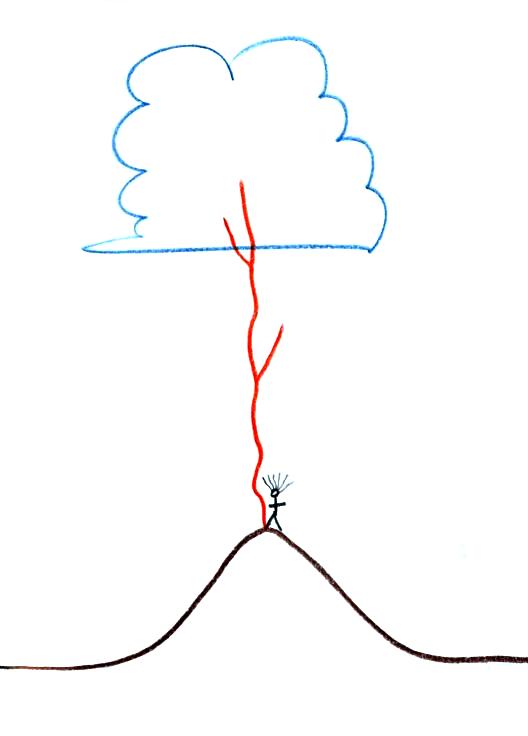
Enhancement of the E field at the top of a
mountain (or tall building or structure) is sometimes high
enough to trigger lightning also.
Note the direction of the branching. This indicates that
this discharge began with a leader process that traveled upward
from the mountain. Most cloud to ground lightning discharges
begin with a leader that propagates from the cloud downward toward
the ground. We will of course look at the events that occur
during lightning discharges in a lot more detail later in the
semester. Here are some
examples filmed in Germany (probably developing off tall
towers of some kind) and strikes to
the Empire State Building.
And finally the ability of a point to draw off or throw off
electrical charged that so interested Benjamin Franklin involves
enhancement of the E field.
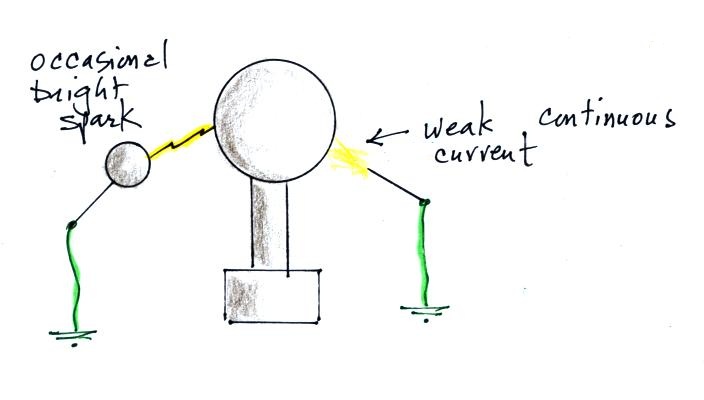
A pointed conductor brought near a Van de Graaff generator
enhances the field enough to ionize air and create charge carries
in the air. A weak current flows between the Van de Graaff
and the point. Charge on the generator is not able to build
to the point where a large bright spark occurs.
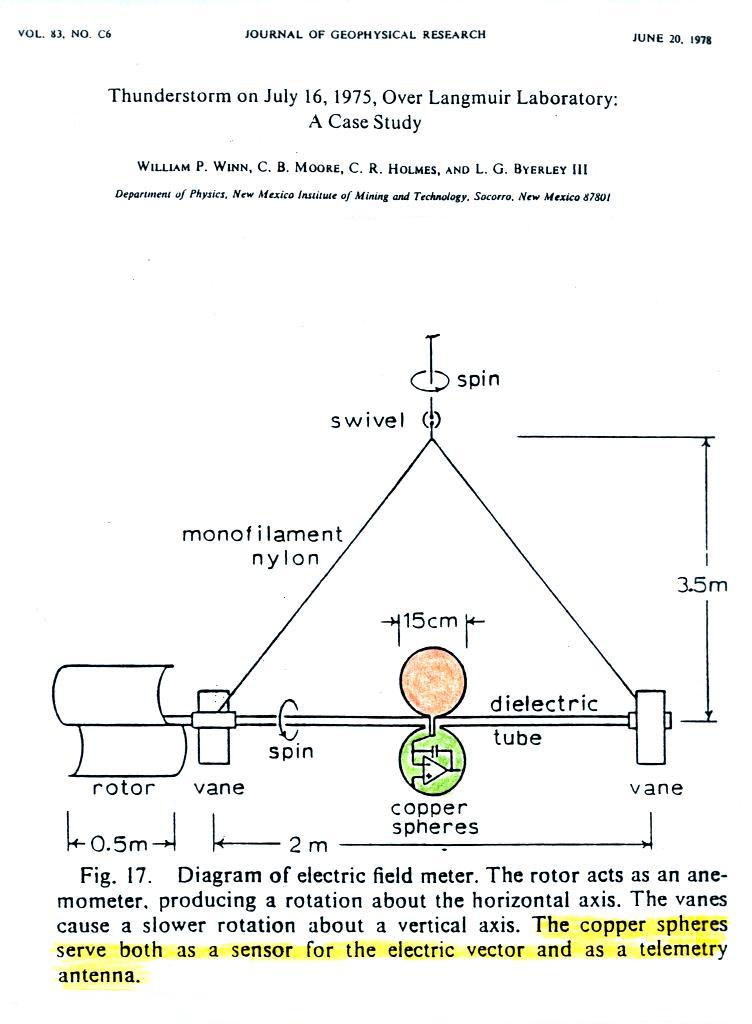
Here's an example of a very cleverly designed
instrument that has been used to measure electric fields above
the ground and inside thunderstorms (you can download the
complete Winn et al. 1978 publication here).
Two metal spheres are attached to and spin
vertically around a horizontal shaft (the shaft also spins
azimuthally). The instrument is launched under a
thunderstorm and is carried upward by balloon.
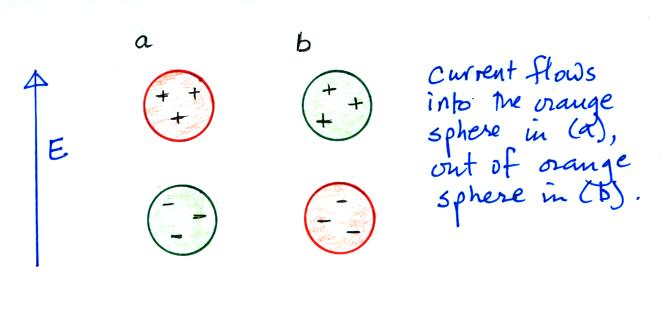
As the spheres spin, a current will move back
and forth between them. The amplitude of the current will
depend on the charge induced on the spheres by the electric
field. The induced charge will, in turn, depend on the
intensity of the E field.
Determining how the two conducting spheres will
enhance the electric field is a more complex problem than we
considered in the last lecture but it has been worked out
analytically (don't worry we won't be looking at the
details). You could also work it out numerically or
determine the enhancement experimentally. Note that the
two spheres also act an antenna for transmitting data back to
the ground.
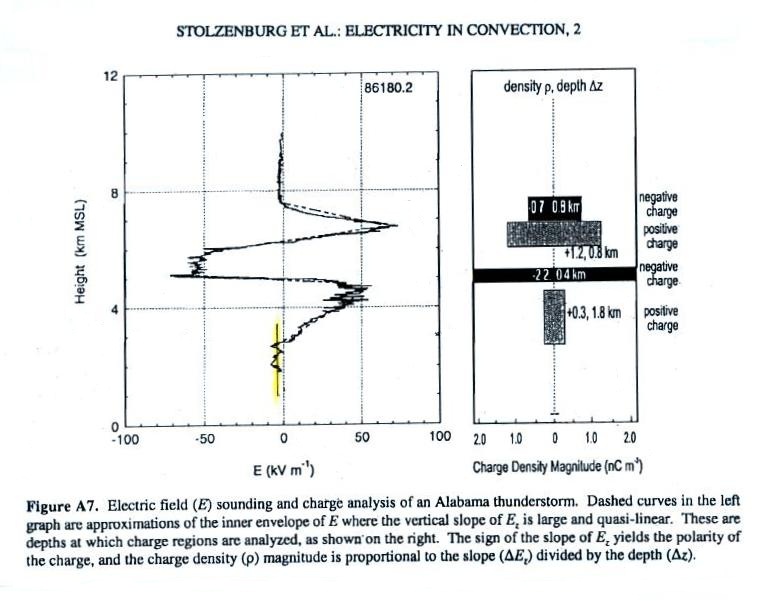
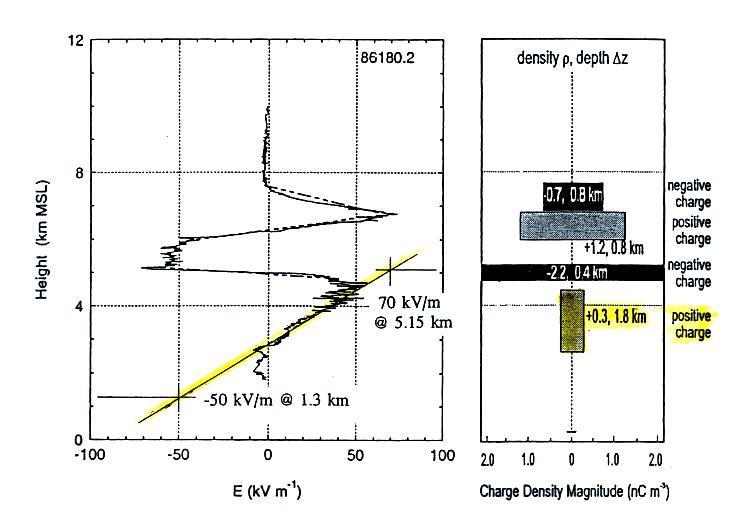
The next figure shows an example of data obtained with an
instrument like this (it is from a different publication which
you can download here,
but a similar instrument was used).
We're going to take a more careful look at 2 or 3 parts of the
E field plot. First the small highlighted portion at the
bottom of the plot. Here the sensor was below the lowest
charge layer in the cloud (perhaps even below the base of the
cloud) and the E field seems to be fairly constant varying between
about -2 and -4 kV/m. Can we use the charge density
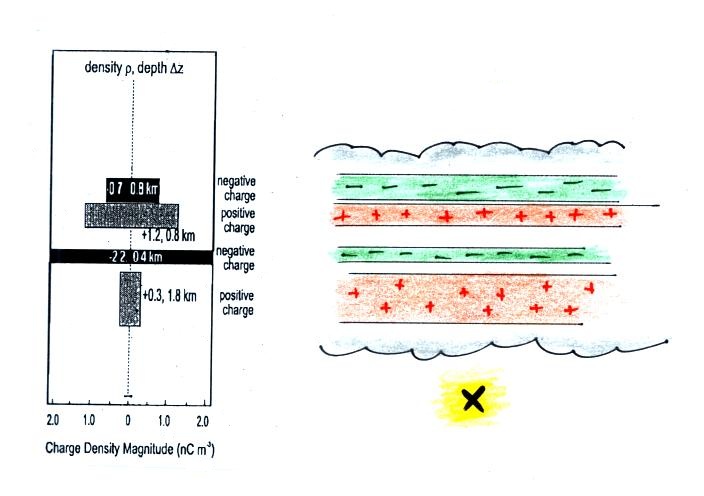
information at right in the figure to explain this field?
There are 4 layers of charge. The field at Pt. X below
the lowest layer will be a superposition of the fields from each
of the layers above. We'll assume each of the layers
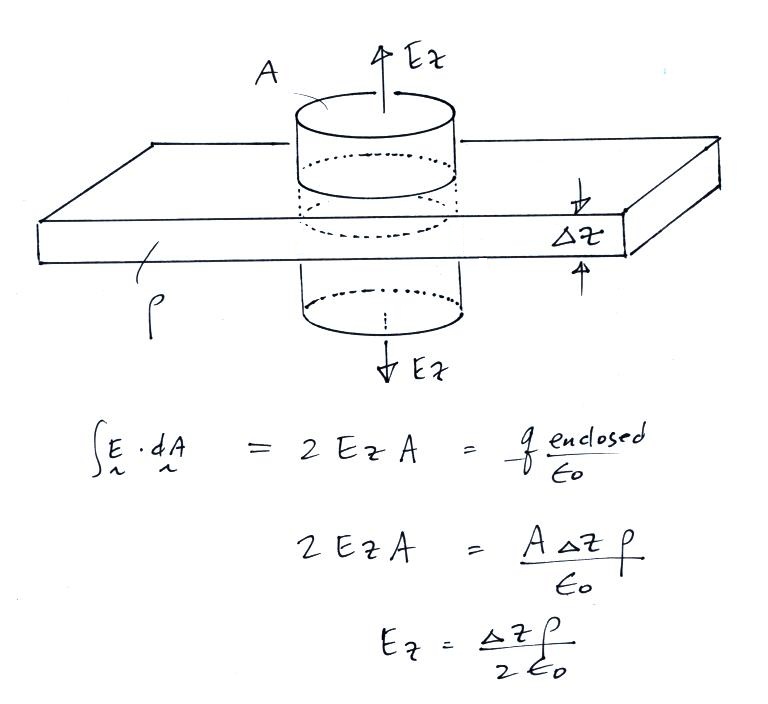
is of infinite horizontal extent. We can use the integral
form of Gauss' Law to determine the field above and below a layer
of charge.
I think you can argue "by inspection" that the field above and
below the infinite layer of charge will have just a
z-component. Also because the layer is of infinite extent
the field strength will be the same at any distance above or below
the layer.
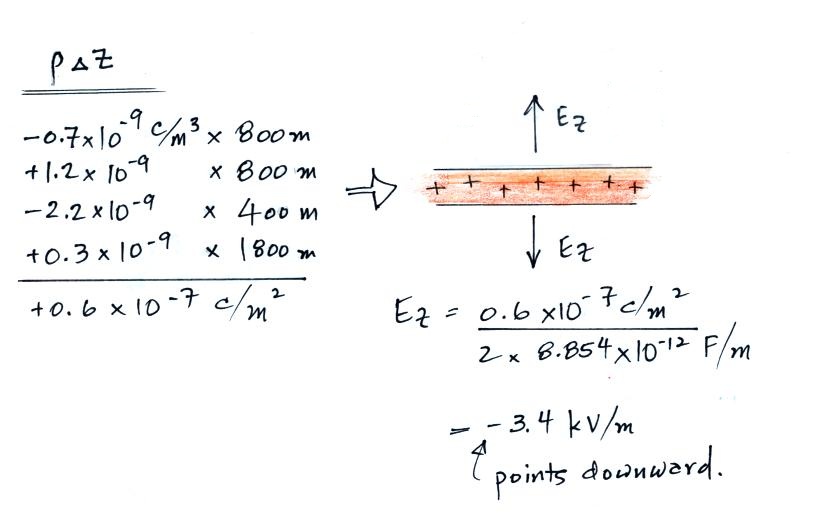
So we compute ρ Δz for each of the layers, add the results
together and use that to compute the field using the equation
above.
Below the cloud we find that the field is negative (points
downward) and has an amplitude of 3.4 kV/m. This agrees very
well with what is shown in the E field sounding.
Next we'll examine that E field change as the sensor
passes through the lowest layer of charge.
We can measure the slope of the field change and the differential
form of Gauss' Law to determine the volume space charge density.
Note that dE/dz is positive on the E field sounding between about
2.7 km and 4.5 km or so. This coincides with a 1.8 km thick
layer of positive space charge. The slope turns negative
between about 4.7 km and 5.1 km where there is a layer of negative
charge. The E field reaches a peak positive value at about
4.6 km, a point that is in between the layers of positive and
negative charge.
We can determine the slope of the line highlighted in yellow and
use that to determine the average volume space charge density in
the layer of positive charge.
The value we obtain (0.27 nC/m3)
is in good agreement with the 0.3 nC/m3 value
given in the paper.