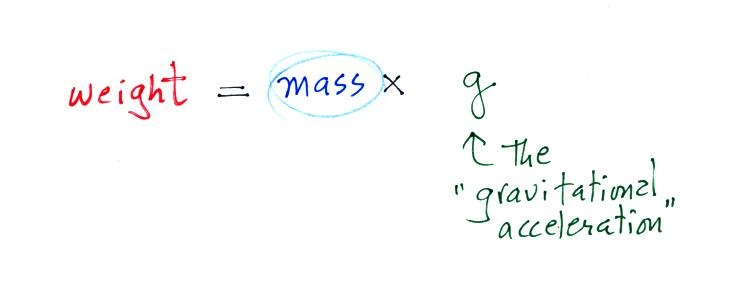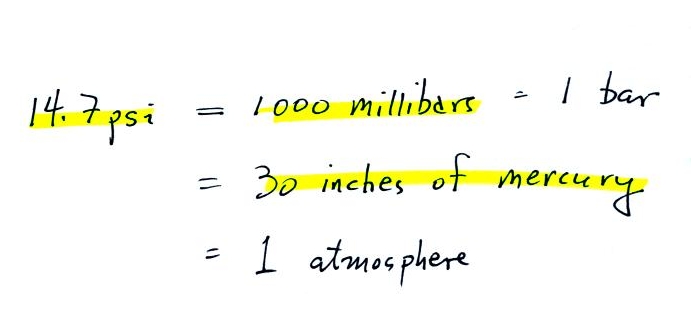Thu., Jan. 29 notes

Thursday Jan. 29, 2015

Music from Dessa this morning: I played all of the following songs in the half hour leading up to the 9:30 am class: "551", "Call Off Your Ghosts", "Skeleton Key", "Mineshaft II", "Dixon's Girl", and "Sadie Hawkins". There was only enough time for three or four before the 8 am class and I don't remember for sure which ones they were. And you should really listen to Dessa discuss what it takes to write and sing songs of this style.

The Practice Quiz is one week from today (Thu., Feb. 5). I will try to get a study guide online one week before each of this semester's quizzes. So here is a preliminary version of the Practice Quiz Study Guide. There may be some small changes made by early next week, because it's not clear at this point whether we will be able to get through the last topic or two on the study guide by the end of class next Tuesday. There will be reviews Tuesday and Wednesday afternoon next week even though this is just a practice quiz.

All the weather prediction models are forecasting a rainy Friday and Saturday. I showed one of the model predictions in class. Here are the current US Weather Service forecasts for Friday through Saturday. They show the probability of precipitation. Up to 1 inch of rain is expected in the Tucson area.


90% chance of rain Thursday night	During the day on Friday	Friday night	Saturday morning	Saturday afternoon and evening

It looks like the rain will stop in time for my Sunday morning bicycle ride.

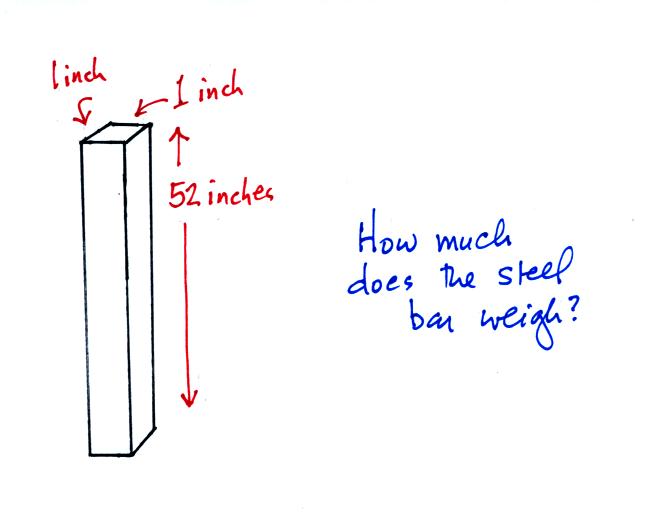
Today's class was all (perhaps too much so) about mass, weight, density, and especially pressure. Weight is something you can feel so I passed an iron bar around in class (it's sketched below). You were supposed to estimate it's weight. The fact that it was 1" by 1" is significant. More about the bar later in today's notes.

A couple of small plastic bottles were passed during class. One contained some water the other an equal volume of mercury (here's the source of the nice photo of liquid mercury below at right). I wanted you to appreciate how much heavier and denser mercury is than water.

Thanks for being careful with the mercury. A spill would have shut down the classroom and perhaps more of the building until the hazardous materials people could come in and clean it up. It isn't so much the liquid mercury that is a hazard, but rather the mercury vapor. Mercury vapor is used in fluorescent bulbs (including the new energy efficient CFL bulbs) which is why they need to be disposed of carefully. That is something we'll mention again later in the class.

I am hoping that you will remember and understand the following statement

atmospheric pressure at any level in the atmosphere
depends on (is determined by)
the weight of the air overhead

We'll first review the concepts of mass, weight, and density. I've numbered the various sections (there are a total of 8) to help with organization.

1. weight
A good place to start because we are most familiar with this term. We can feel weight and we routinely measure weight.

A person's weight also depends on something else.

In outer space away from the pull of the earth's gravity people are weightless. Weight depends on the person and on the pull of gravity.

We measure weight all the time. What units do we use? Usually pounds, but sometimes ounces or maybe tons. Several people mentioned grams or kilograms. Technically those are units of mass, but, as we will see, we can use kilograms and pounds interchangeably on the surface of the earth.

Speaking of mass

2. mass
Mass is a better way of expressing the amount of matter in an object.

Grams (g) and kilograms (kg) are commonly used units of mass (1 kg is 1000 g).

3. gravitational acceleration

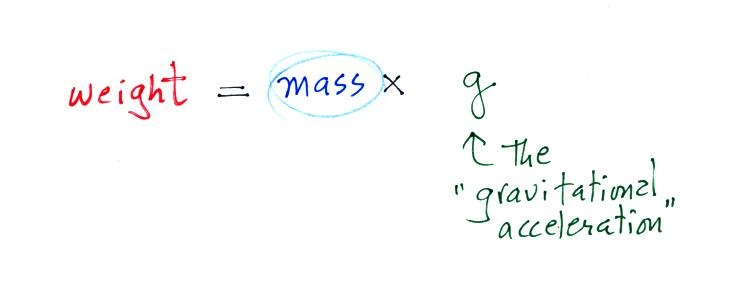
On the surface on the earth, weight is mass times a constant, g, known as the gravitational acceleration. The value of g is what tells us about the strength of gravity on the earth; it is determined by the size and mass of the earth. On another planet the value of g would be different. If you click here you'll find a little (actually a lot) more information about Newton's Law of Universal Gravitation. You'll see how the value of g is determined and why it is called the gravitational acceleration. These aren't details you need to worry about but I feel they should be available in case you're curious.

Here's a question to test your understanding.

The masses are all the same. On the earth's surface the masses would all be multiplied by the same value of g. The weights would all be equal. If all 3 objects had a mass of 1 kg, they'd all have a weight of 2.2 pounds. That's why we can use kilograms and pounds interchangeably.

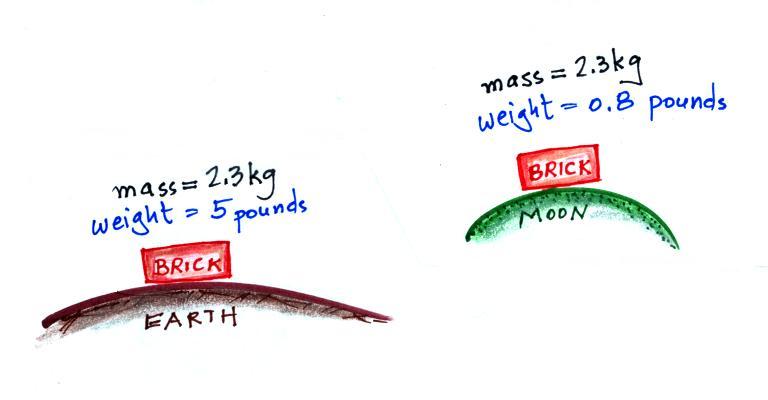
The following figure show a situation where two objects with the same mass would have different weights.

On the earth a brick has a mass of about 2.3 kg and weighs 5 pounds. If you were to travel to the moon the mass of the brick wouldn't change (it's the same brick, the same amount of stuff). Gravity on the moon is weaker (about 6 times weaker) than on the earth because the moon is smaller, the value of g on the moon is different than on the earth. The brick would only weigh 0.8 pounds on the moon. The brick would weigh almost 12 pounds on the surface on Jupiter where gravity is stronger than on the earth.

The three objects below were not passed around class (one of them is pretty heavy). The three objects all had about the same volumes. One is a piece of wood, another a brick, and the third something else.

You could probably have determined which one was a brick because there were some unwrapped bricks on the table. You could compare the volumes. To distinguish between the other two you'd either have to pick them up (one was much heavier than the other) or, as suggested in the 9:30 class, stand them on end and tip them over (the heavier object made a much louder noise when it fell).

The point of all this was to get you thinking about density. Here we had three objects of about the same size with different weights. That means the objects had different masses (since weight depends on mass). The three different masses, were squeezed into roughly the same volume producing objects of very different densities.

4. density

The brick in the back weighed about 5 pounds, the piece of wood about 1 pound. The third object was made out of lead and weighed 15 pounds, it had the highest density by far.

We'll be more concerned about air in this class than wood, brick, or lead.

In the first example below we have two equal volumes of air but the amount in each is different (the dots represent air molecules).

The amounts of air (the masses) in the second example are the same but the volumes are different. The left example with air squeezed into a smaller volume has the higher density.

material	density g/cc
air	0.001
redwood	0.45
water	1.0
iron	7.9
lead	11.3
mercury	13.6
gold	19.3
platinum	21.4
iridium	22.4
osmium	22.6

g/cc = grams per cubic centimeter
one cubic centimeter is about the size of a sugar cube

I wish I could get my hands on some iridium or osmium just to be able to feel how heavy they are.

Here's a more subtle concept. What if we were in outer space with the three wrapped blocks of lead, wood, and brick. They'd be weightless.
Could we tell them apart then? They would still have very different densities and masses but we wouldn't be able to feel how heavy they were.

5. inertia

I think the following illustration will help you to understand inertia.

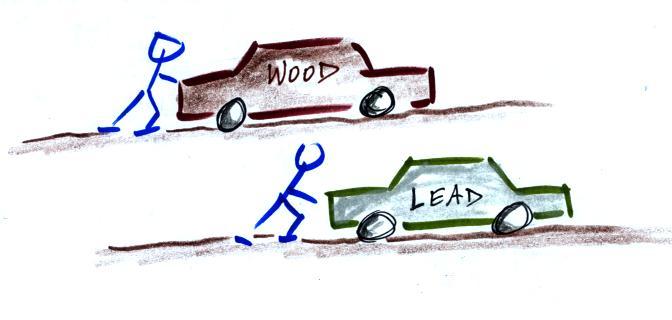
Two stopped cars. They are the same size except one is made of wood and the other of lead. Which would be hardest to get moving (a stopped car resists being put into motion). It would take considerable force to get the lead car going. Once the cars are moving they resist a change in that motion. The lead car would be much harder to slow down and stop.

This is the way you could try to distinguish between blocks of lead, wood, and brick in outer space. Give them each a push. The wood would begin moving more rapidly than the block of lead even if both are given the same strength push.

This concept of inertia comes from Newton's 2nd law of motion

F = m a

F is force, m is mass, and a is acceleration. We can rewrite the equation

a = F/m

This shows cause and effect more clearly. If you exert a force (cause) on an object it will accelerate (effect). Acceleration can be a change in speed or a change in direction (or both). Because the mass is in the denominator, the acceleration will be less when mass (inertia) is large.

Here's where we're at

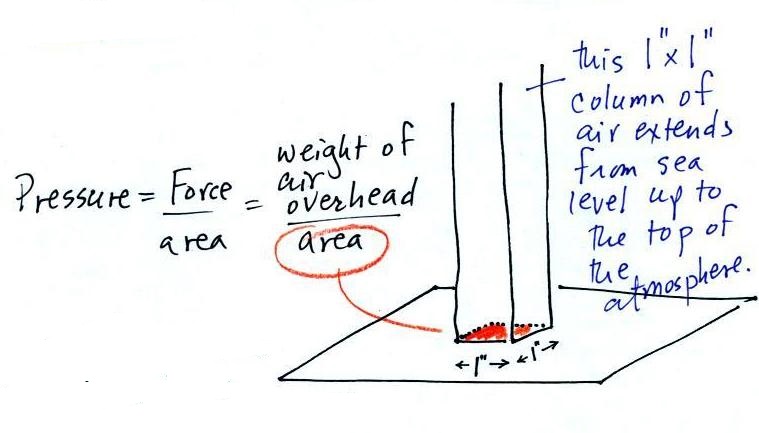
The weight of the iron bar is still unknown.

A very tall 1 inch x 1 inch column of air has been added to the picture. Other than being a gas, being invisible, and having much lower density it's really no different from the other objects.

Now we're ready to define (and hopefully understand) pressure. It's a pretty important concept. A lot of what happens in the atmosphere is caused by pressure differences. Pressure differences cause wind. Large pressure differences (such as you might find in a tornado or a hurricane) can create strong and destructive storms.

The air that surrounds the earth has mass. Gravity pulls downward on the atmosphere giving it weight. Galileo conducted a simple experiment to prove that air has weight (in the 1600s). The experiment wasn't mentioned in class.

Atmospheric pressure at any level in the atmosphere
depends on (is determined by)
the weight of the air overhead

This is one way, a sort of large, atmosphere size scale way, of understanding air pressure.

6. pressure

and here we'll apply the definition to a column of air stretching from sea level to the top of the atmosphere

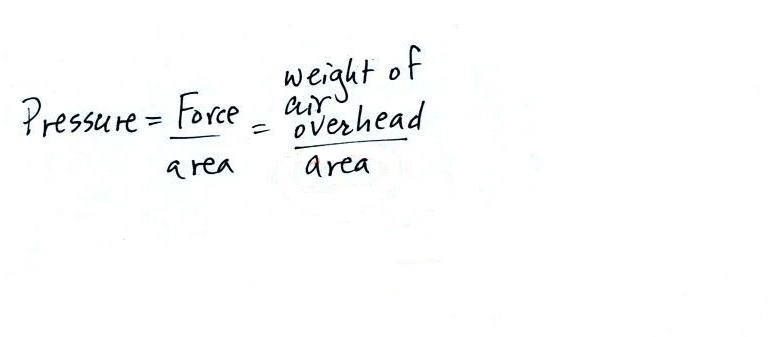
Pressure is defined as force divided by area. Atmospheric pressure is the weight of the air column divided by the area at the bottom of the column (as illustrated above).

Under normal conditions a 1 inch by 1 inch column of air stretching from sea level to the top of the atmosphere will weigh 14.7 pounds. Normal atmospheric pressure at sea level is 14.7 pounds per square inch (psi, the units you use when you fill up your car or bike tires with air).

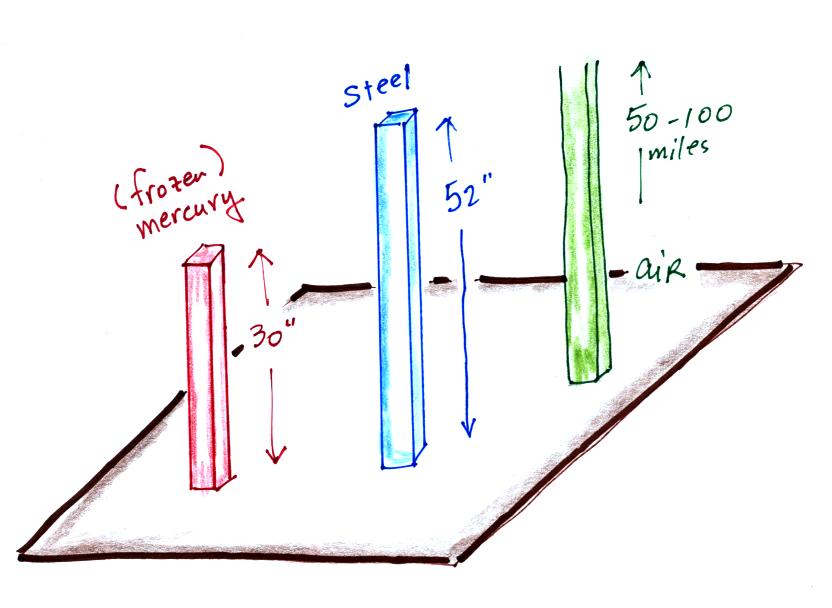
Now back to the iron bar. A lot of people felt it weighed more than 20 pounds. The bar actually weighs 14.7 pounds. When you stand the bar on end, the pressure at the bottom would be 14.7 psi.

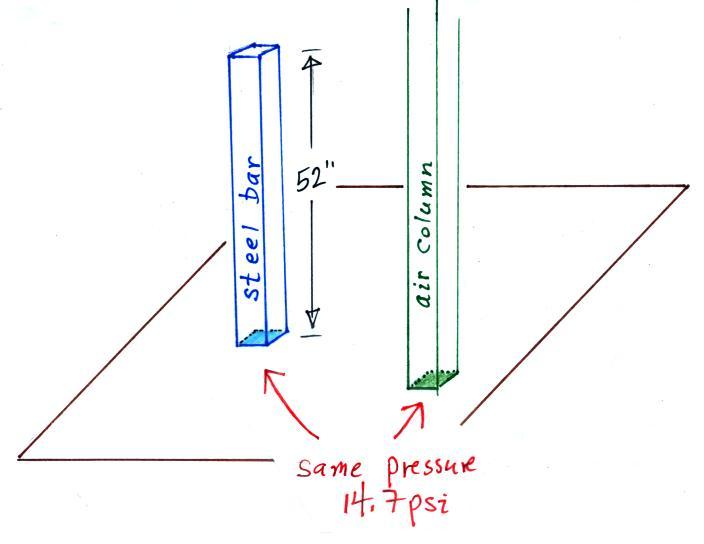
The weight of the 52 inch long 1" x 1" steel bar is the same as a 1" x 1" column of air that extends from sea level to the top of the atmosphere 100 or 200 miles (or more) high. The pressure at the bottom of both would be 14.7 psi.

7. pressure units

Pounds per square inch, psi, are perfectly good pressure units, but they aren't the ones that most meteorologists use.

Typical sea level pressure is 14.7 psi or about 1000 millibars (the units used by meteorologists and the units that we will use in this class most of the time) or about 30 inches of mercury. Milli means 1/1000 th. So 1000 millibars is the same as 1 bar. You sometimes see typical sea level pressure written as 1 atmosphere.

Inches of mercury refers to the reading on a mercury barometer. This seems like unusual units for pressure. But if you remember the chart earlier, Mercury (13.6 grams/cm³) is denser than steel ( about 7.9 grams/cm³ ). If we could some how construct a 1" x 1" bar of mercury it would need to be 30 inches long to equal the weight or the iron bar or the weight of a tall column of air.

Each of these columns would weigh 14.7 pounds. The pressure at the base of each would be the same.

A mercury barometer is, we'll find, just a balance. You balance the weight of a very tall column of air with the weight of a much shorter column of mercury.

Someone asked about the freezing point of mercury after class. It's not all that cold -38 C which is about -39 F. Alcohol is often used in thermometers in cold locations to avoid having the mercury freeze (and break the thermometer).

You never know where something you learn in ATMO 170A1 will turn up. I once lived and worked for a short time in France. Here's a picture of a car I owned when I was there (this one is in mint condition, mine was in far worse shape)

It's a Peugeot 404. After buying it I took it to the service station to fill it with gas and to check the air pressure in the tires. I was a little confused by the air compressor though, the scale only ran from 0 to 3 or 4. I wanted to put about 30 psi into the tires but the scale on the compressor only went up to 4. After about 15 minutes I realized the compressor was marked in "bars" not "psi". Since 14.7 psi is about 1 bar, 30 psi would be about 2 bars.

You can learn a lot from bricks

For example the photo below (taken in my messy office) shows two of the bricks from class. One is sitting flat, the other is sitting on its end. Each brick weighs about 5 pounds. Would the pressure at the base of each brick be the same or different in this kind of situation?

Pressure is determined by (depends on) weight so you might think the pressures would be equal. But pressure is weight divided by area. In this case the weights are the same but the areas are different. In the situation at left the 5 pounds must be divided by an area of about 4 inches by 8 inches = 32 inches. That works out to be about 0.15 psi. In the other case the 5 pounds should be divided by a smaller area, 4 inches by 2 inches = 8 inches. That's a pressure of 0.6 psi, 4 times higher.

Here's a picture of 5 bricks stacked on top of each other. It's kind of like layers of air in the atmosphere.

Each of the bricks weighs 5 pounds, there's a total of 25 pounds of weight. Divide that by the 32 square inch area at the bottom of the pile and yet get less than 1 psi. That's a lot lower than atmospheric pressure. You'd need a 94 brick tall pile of bricks (470 pounds of bricks) to equal atmospheric pressure.

The main reason I brought the bricks was so that you could understand what happens to pressure with increasing altitude.

At the bottom of the pile you would measure a weight of 25 pounds. If you moved up a brick you would measure a weight of 20 pounds, the weight of the four bricks that are still above. The pressure would be less. Weight and pressure will decrease as you move up the pile.

8. pressure changes with altitude

Layers of air in the atmosphere is not too much different from a pile of bricks. Pressure at any level is determined by the weight of the air still overhead. Pressure decreases with increasing altitude because there is less and less air remaining overhead.

At sea level altitude, at Point 1, the pressure is normally about 1000 mb. That is determined by the weight of all (100%) of the air in the atmosphere.

Some parts of Tucson, at Point 2, are 3000 feet above sea level (most of central Tucson is a little lower than that around 2500 feet). At 3000 ft. about 10% of the air is below, 90% is still overhead. It is the weight of the 90% that is still above that determines the atmospheric pressure in Tucson. If 100% of the atmosphere produces a pressure of 1000 mb, then 90% will produce a pressure of 900 mb.

Pressure is typically about 700 mb at the summit of Mt. Lemmon (9000 ft. altitude at Point 3) because 70% of the atmosphere is overhead..

Pressure decreases rapidly with increasing altitude. We will find that pressure changes more slowly if you move horizontally. Pressure changes about 1 mb for every 10 meters of elevation change. Pressure changes much more slowly normally if you move horizontally: about 1 mb in 100 km. Still the small horizontal changes are what cause the wind to blow and what cause storms to form.

Point 4 shows a submarine at a depth of about 30 ft. or so. The pressure there is determined by the weight of the air and the weight of the water overhead. Water is much denser and much heavier than air. At 30 ft., the pressure is already twice what it would be at the surface of the ocean (2000 mb instead of 1000 mb).

Here are a couple of links that I forgot to include in the notes for class. The first is about the relatively new sport of free diving. The 2nd is a link to an article about a diver that made it to a depth of 236 feet but died upon reaching the surface. The divers hold their breath and must descend and return to the surface on just a single lungful of air. Death was caused by the high pressure deep under water forcing fluid from the blood into the diver's lungs.

In the 9:30 class I kept a running list of the main ideas we covered in today's class. Here's what we ended up with