Diffusion theory does a pretty good job of describing the attachment of small ions to uncharged particles.  The first step will be to solve the diffusion equation

The geometry and the boundary conditions are shown below


We'll consider just a single uncharged particle surrounded by small ions.  The particle has a radius of a.  The small ion concentration zero at the surface of the particle where the small ions are collected.  Far from the particle the small ion concentration is n∞

We assume a steady state small ion concentration


We'll use spherical geometry for this problem with the coordinate axes centered on the particle.  Because of the spherical symmetry there is no θ or φ dependence, we need to consider only the r dependence.  The Laplacian becomes

This is an easy equation to solve

Now we make use of the two boundary conditions.  First, far from the particle (r approaches infinity) the small ion concentration should be n∞.


Then at the surface of the particle the small ion concentration is zero

So the solution is


Now that we know n(r) we can determine the flux (particles passing through unit area per unit of time) of small ions toward the particle.  This depends on the gradient of n(r)


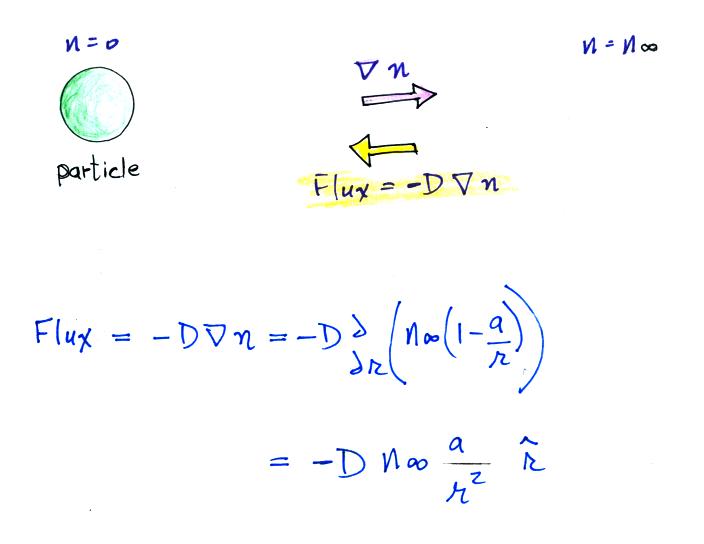
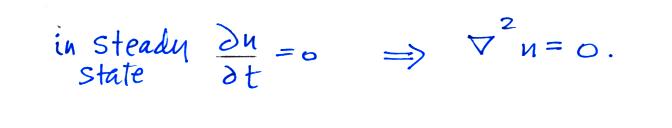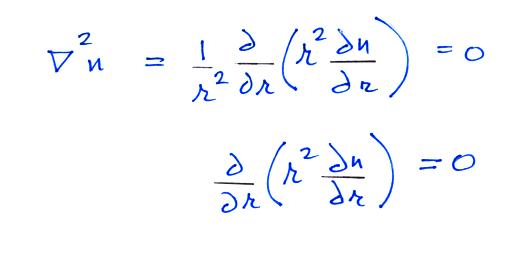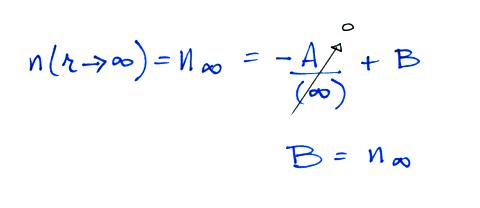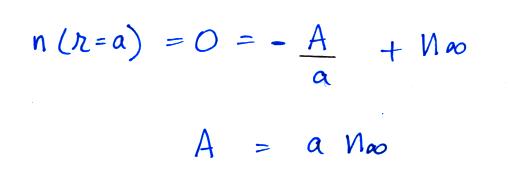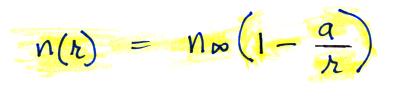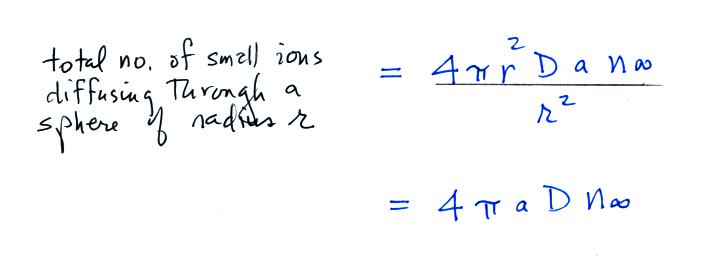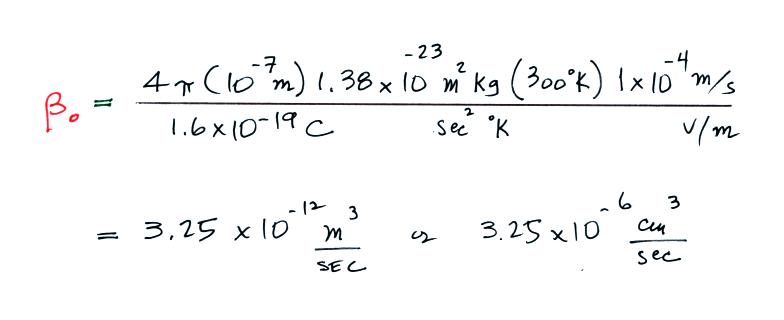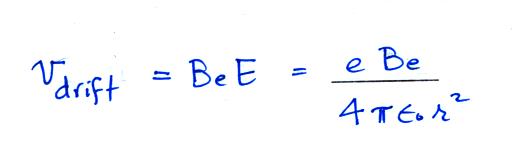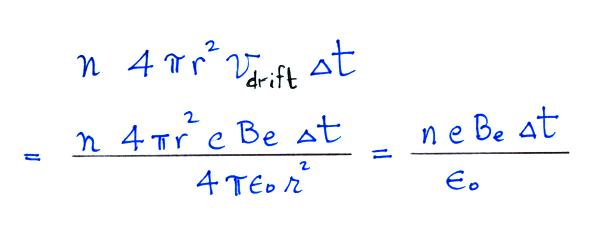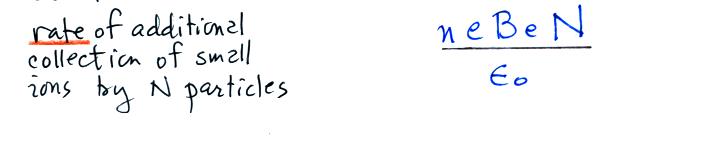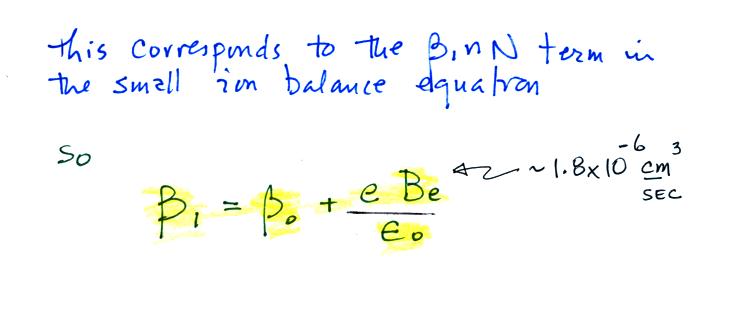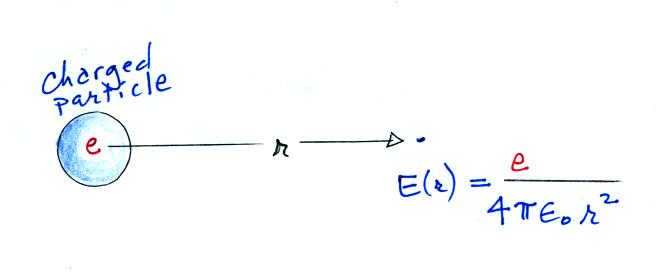
Next we find the total number of particles moving inward toward the particle by multiplying the flux by the area of a sphere with radius r surrounding the particle

We assume these small ions are all collected by the particle.  We've only considered a single particle at this point, so to determine the total rate of loss of small ions we need to multiply by the concentration No of uncharged particles.

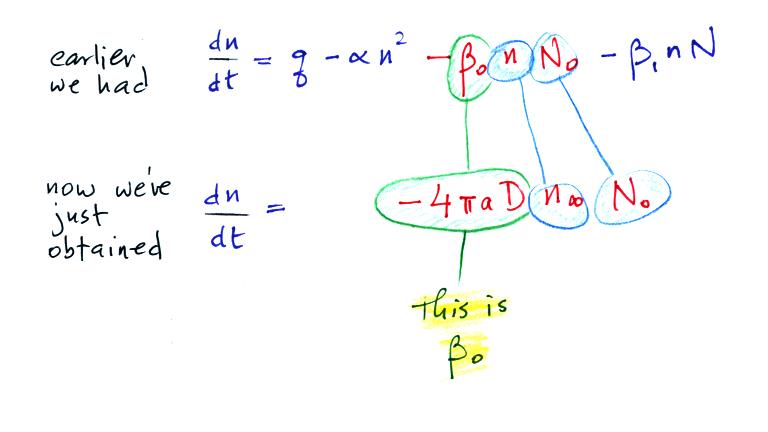
Now let's go back and write down the small ion balance equation again


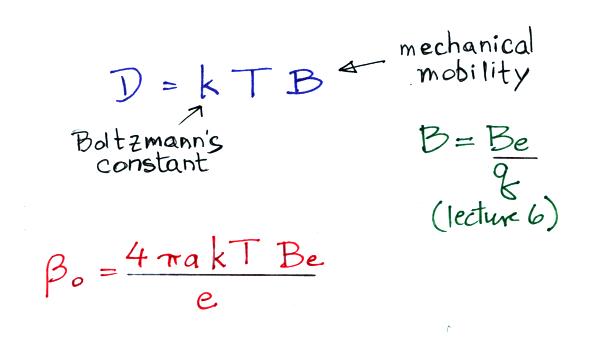
By comparing the small ion loss expression we've just derived with the corresponding term in the small ion balance equation we can see that βo  =  4 π a D

An expression for the diffusion coefficient, D, can be derived using principles from kinetic theory and is

The top expression above is also know as the Einstein (or Einstein-Smoluchowski) Relation.
Here's an example calculation where we assume a particle radius of 0.1 μm (10-7 m) and an electrical mobility of 1 x 10-4 (m/s)/(V/m).


Now we will look at the collection of small ions by a charged particle.  Diffusion will still be involved but we will need to add an additional term that accounts for the movement of small ions caused by the influence of the electrical field surrounding the particle.

First the E field surrounding a charged particle (the charge on the particle can only be multiples of an electronic charge, we assume just a single electronic charge in the figure below)


The drift velocity due to this E field is

Now we will multiply n, the concentration of small ions, by the area of a sphere of radius r surrounding the charged particle and by vdrift Δt, the distance the small ions will move in time Δt.  This will be the number of small ions that pass through the sphere in time Δt.

Now we'll multiply by N, the concentration of charged particles and divide by Δt to get the rate of attachment of small ions to charged particles due to the influence of the particle's electric field.


To find the total rate of collection by the charged particles we need to add in the diffusive loss term.  So we have

Together the two terms in this expression correspond to the β1nN term in the small ion balance equation.  From that we get the following expression for β1


One last item before we leave this supplementary lecture - a table comparing values of β0 and β1 


particle radius (μm)
βo (cm3/sec)
 β1 (cm3/sec)
0.01
 3.25 x 10-7
 2.12 x 10-6
0.05
 1.62 x 10-6 3.42 x 10-6
0.1
 3.25 x 10-6 5.05 x 10-6
0.2
 6.5 x 10-6 8.3 x 10-6
0.5
 1.62 x 10-5
 1.8 x 10-5
1.0
 3.25 x 10-5 3.43 x 10-5


It appears that β1 becomes dominant for particles with small radii.  For larger particles β0 = β1