Click here to download this material in a more printer friendly format

We need to try to learn a little bit more about saturation of air.  In particular why is there an upper limit to the amount of water vapor that can be found in air and why does that saturation amount depend on temperature?

The first thing we need to realize is that warm water will evaporate more rapidly than cool water.  You probably know that already.  If a cup of iced tea were set next to a cup of hot tea you probably be able to tell which was which by just looking at them.  You wouldn't need to touch or taste the tea or look for ice cubes in the iced tea.

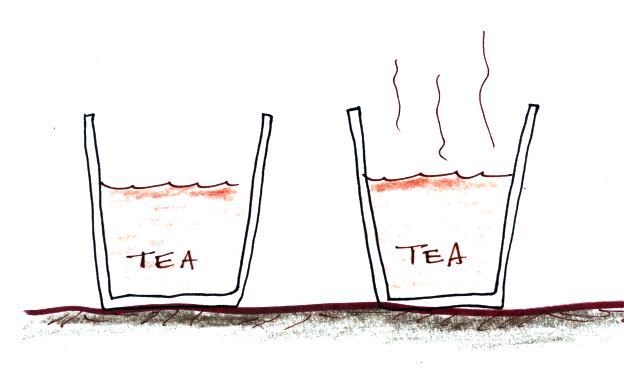
You might notice that one of the cups of tea was steaming (the cup on the right above).  This would be the hot tea.  You're not actually seeing water vapor.  Rather water vapor is evaporating so quickly that it is saturating the air above.  The air isn't able to accommodate that much water vapor and some of it condenses and forms a cloud of steam.  That's what you are seeing.

Now we'll redraw the picture and cover both cups so that water vapor can begin to buildup in the air above the water in both cups.
 

Arrows represent the different rates of evaporation.  One arrow is shown evaporating from the cup of cold water.  We'll just assume the warmer water at right is evaporating 3 times more rapidly.  We've arbitrarily assigned rates of evaporation of 10 and 30 to the water in the two cups.  The actual numbers aren't important, the important point is that the warm water evaporates more quickly than the cold water.

Water vapor will start to buildup in the air above each cup.  And, even though it has just evaporated, some of the water vapor will condense and rejoin the water at the bottom of each cup.  Let's just assume that 1% of the water vapor molecules will condense (again just a made up number).

The amount of water vapor in each glass will increase until it reaches a point where
water evaporation rate = water vapor condensation rate

for the cup of cold water
10 = 0.01 x water vapor concentration

The 0.01 is 1% expressed in decimal form.  Solving this equation gives you a water vapor concentration of 1000.  The air is saturated when you reach this point and the RH = 100%.


The saturation water vapor concentration in the air in the warm cup would be 3000.  And again the relative humidity would be 100%.

The air is saturated in both glasses but there is more water vapor in the warm glass.

The fact that the rates of evaporation and condensation are equal when air is saturated (RH = 100%) is something we'll be using later when we study the formation of precipitation.  Here's a picture of how that would look inside a cloud.

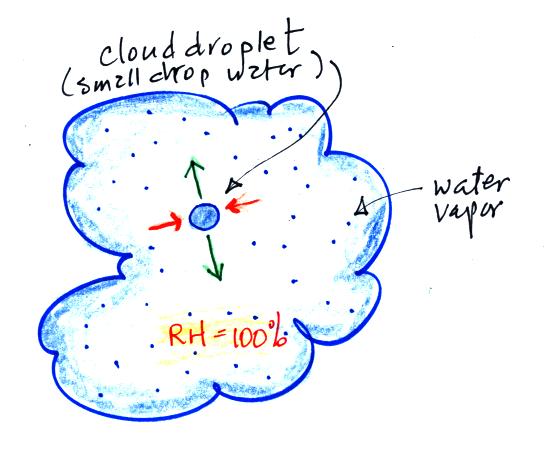
The air inside the cloud is saturated.  The rate of evaporation from the cloud droplet (2 green arrows) is balanced by an equal rate of condensation (2 orange arrows).  The RH = 100%.  The cloud droplet won't grow any bigger or get any smaller.

Here's something to test your understanding of this material.  As a matter of fact I'll make it an Optional Assignment.  Turn in your answers to the questions below at the start of class on Wed., Mar. 20 and you'll receive some extra credit.


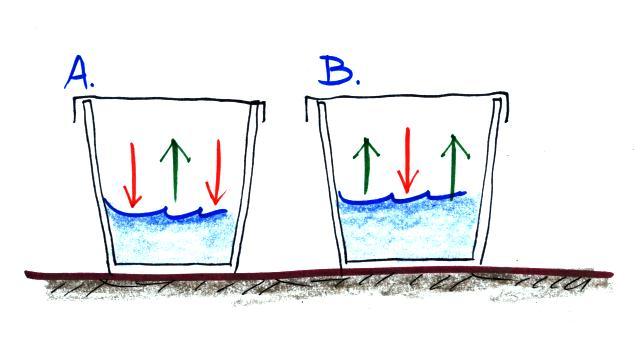
What information can you add to this picture?  Is the water in Glass A  WARMER  or  COLDER  than in Glass B?  Is there MORE  or  LESS  water vapor in the air in Glass A than in Glass B?  Is the relative humidity in each glass MORE than 100%, LESS than 100% or is it EQUAL to 100%.  The rates of evaporation and condensation aren't equal in either glass, so the pictures will change with time.  What will the glasses look once they have reached equilibrium? 

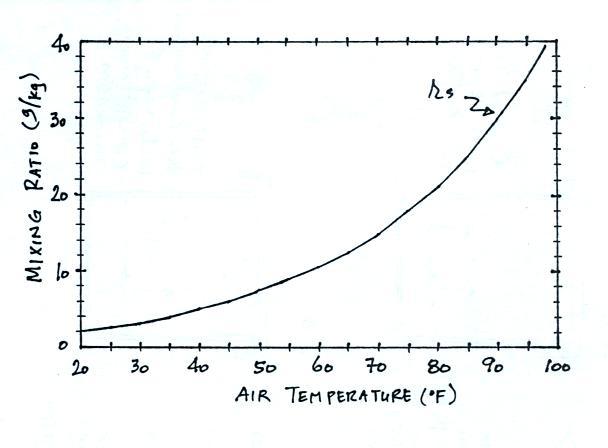
We'll end this section with a table that shows the dependence of saturation mixing ratio on air temperature.

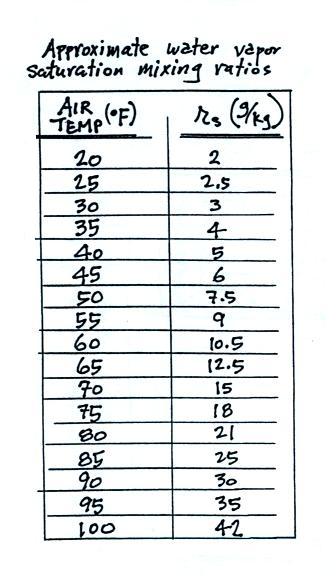
Note that the value of the saturation mixing ratio doubles for every 20 F increase in temperature.  The same data are shown in graphical form below.