Thu., Feb. 10 notes

And some historical information (that was on a class handout). It really was the study of atmospheric electricity (studies of ionization of air) that lead to the discovery of cosmic radiation.

I briefly mentioned a relic from the Cold War - a Nu-Klear Fallout Detector. In many ways it is similar to the electrometers described above and I would love to be able to bring it to class. I used to have one but it has been lost. If you happen to find one for sale somewhere, please let me know.

The following information on ionization rates at various altitudes above the ground was actually on a handout distributed in class on Tuesday.

This first figure shows ionization rates in the first meter above the ground (source: E.T. Pierce, "Some Topics in Atmospheric Electricity," in Recent Advances in Atmospheric Electricity, Proc. 2nd Conf. on Atmospheric Electricity, ed. by L.G. Smith, 1958)

This second figure extends from essentially ground level up to 10 km altitude (source: W.A. Hoppel, R.V. Anderson, J.C. Willett, "Atmospheric Electricity in the Planetary Boundary Layer," ch. 11 in The Earth's Electrical Environment, National Academy Press, 1986 (the "yellow book).

Here is some information on cosmic ray showers. Very few of the primary particles reach the ground. Rather they interact with gas molecules in the atmosphere and produce a wide variety of types of secondary particles. (source: http://www.mpi-hd.mpg.de/hfm/CosmicRay/Showers.html )

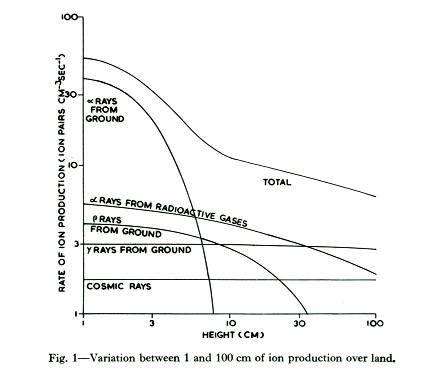
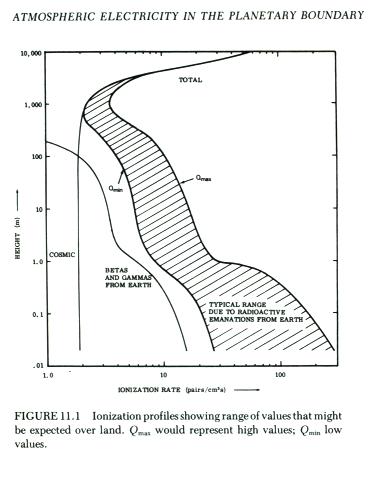
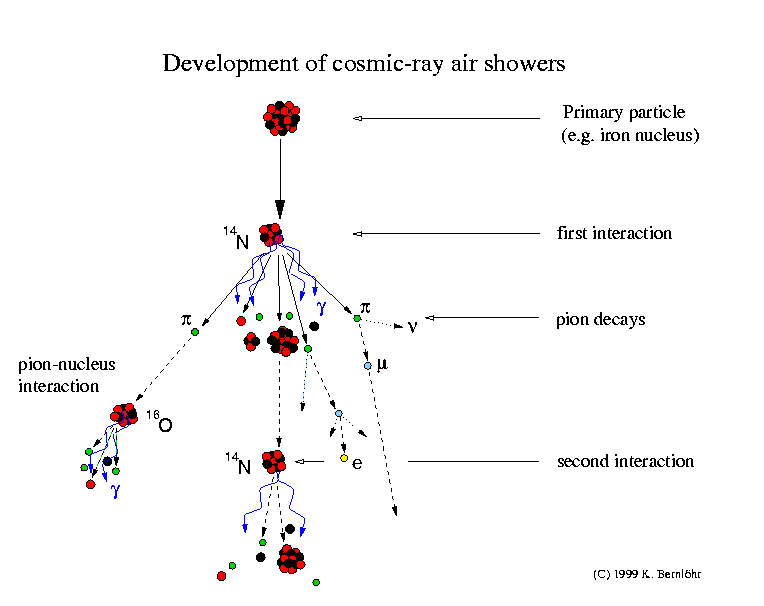
Cosmic-ray air showers

Cosmic rays

The earth is hit by elementary particles and atomic nuclei of very large energies. Most of them are protons (hydrogen nuclei) and all sorts of nuclei up to uranium (although anything heavier than nickel is very, very rare). Those are usually meant when talking about cosmic rays. Other energetic particles in the cosmos are mainly electrons and positrons, as well as gamma-rays and neutrinos.

Interactions and particle production
The cosmic rays will hardly ever hit the ground but will collide (interact) with a nucleus of the air, usually several ten kilometers high. In such collisions, many new particles are usually created and the colliding nuclei evaporate to a large extent. Most of the new particles are pi-mesons (pions). Neutral pions very quickly decay, usually into two gamma-rays. Charged pions also decay but after a longer time. Therefore, some of the pions may collide with yet another nucleus of the air before decaying, which would be into a muon and a neutrino. The fragments of the incoming nucleus also interact again, also producing new particles.

The gamma-rays from the neutral pions may also create new particles, an electron and a positron, by the pair-creation process. Electrons and positrons in turn may produce more gamma-rays by the bremsstrahlung mechanism.

Shower development

The number of particles starts to increase rapidly as this shower or cascade of particles moves downwards in the atmosphere. On their way and in each interaction the particles loose energy, however, and eventually will not be able to create new particles. After some point, the shower maximum, more particles are stopped than created and the number of shower particles declines. Only a small fraction of the particles usually comes down to the ground. How many actually come down depends on the energy and type of the incident cosmic ray and the ground altitude (sea or mountain level). Actual numbers are subject to large fluctuations.

In fact, from most cosmic rays nothing comes down at all. Because the earth is hit by so many cosmic rays, an area of the size of a hand is still hit by about one particle per second. These secondary cosmic rays constitute about one third of the natural radioactivity.

When a primary cosmic ray produces many secondary particles, we call this an air shower. When many thousand (sometimes millions or even billions) of particles arrive at ground level, perhaps on a mountain, this is called an extensive air shower (EAS). Most of these particles will arrive within some hundred meters from the axis of motion of the original particle, now the shower axis. But some particles can be found even kilometers away. Along the axis, most particles can be found in a kind of disk only a few meters thick and moving almost at the speed of light. This disk is slightly bent, with particles far from the axis coming later. The spread or thickness of the disk also increases with distance from the axis.

Shower detection

Extensive air showers with many particles arriving on the ground can be detected with different kinds of particle detectors. In the air the particles may also emit light by two different processes: Cherenkov light almost along the shower axis and fluorescence light in all directions.

Other introductory material found on the net (HTML format):
Cosmic Rays by Richard Mewaldt
Cosmic Rays by James Schombert
Further reading found on the net (Postscript or PDF format):
Particle Data Group: review of cosmic rays
Introduction to high energy cosmic ray physics
Cosmic Ray Spectrum and Composition: Ground Observations

This page was written by Konrad Bernlöhr.

We've looked at some of the sources of radiation that ionize air. When neutral oxygen or nitrogen are ionized you are left with a positively charged N₂ or O₂ molecule and a free electron. The electron subsequently attaches to neutral oxygen molecules (but not to nitrogen). The time that this takes can be calculated in a relatively straight forward way. This was summarized on a class handout.

To estimate the lifetime of a free electron, we need to know the oxygen concentration in air, [O2], and a rate constant k_1.

We can use the ideal gas law equation to determine the oxygen concentration. Electron attachment occurs very quickly, in a few or a few tens of nanoseconds.

The next step in small ion formation is clustering of a chemical species of some kind around the positively and negatively charged ions. This occurs on a millisecond time scale. In the figure above we show ionized nitrogen and oxygen molecules. This is just one possibility. CO₄^- is apparently one of the more common ions found in the centers of these molecular clusters also. And something other than water may envelope the central ion.

The mobilities of positively and negatively charged small ions are slightly different. Typical values are shown above. The positively charged small ions have a slightly higher mobility (slightly lower drift speed) than the negatively charged ions.

What happens to the small ions once they are created. How long do they survive. For that we need an ion balance equation.

The small ion concentration will depend on the ion production rate, q, and the rate at which ions recombine and neutralize each other. In the first equation above that is alpha times the concentration of positive and negative small ions (n₊ and n_-). A somewhat simpler version can be written if we assume that the concentrations of positive and negative small ions are equal.
The next figure gives the general and steady state solutions to the ion balance equation.

We get the steady state concentration as t goes to infinity. At steady state, dn/dt is zero so here's another way of detemining the steady state solution.

How long does it take to get to steady state?

A quick calculation done after class (below) shows that you get to steady state in several minutes.

Next we can calculate the steady state concentration and then the lifetime of a typical small ion (concentration divided by production rate or by recombination rate since they are equal at steady state)

We can also estimate the conductivity (remembering that both positive and negative small ions contribute to the conductivity and taking into account that the positive and negative small ions have slightly different electrical mobilities). We assume that the small ions carry a single electronic charge.