Wednesday Mar. 24, 2010
click here to download today's notes in a more
printer friendly format
2 or 3 songs from Vampire
Weekend's new CD Contra ("Cousins" and "I Think Ur a Contra" maybe).
The Experiment #3 reports are due next Monday. Try to return
your materials this week (either in class or come by my office) so that
you can pick up the Supplementary Information handout.
There is a new Optional
Assignment on humidity that is due next Monday. The two most
recent optional assignments (Controls of Temperature and an inclass
assignment were returned today).
We spent the first part of the period looking at why there is an
upper limit to the amount of water vapor that can be found in air and
why that limit depends on temperature. These notes were stuck
onto end of the Monday Mar. 22 online notes.
The rest
of the period was spent working out some humidity example problems.
This
way
you will learn more about the 4 humidity variables
(mixing ratio, saturation mixing ratio, relative humidity, and dew
point temperature). You'll see what they do and what can cause
their values to change.
Example 1
Here is the first sample
problem that we worked in
class. You might have a hard time unscrambling this if
you're seeing it for
the first
time. The series of steps that we followed are retraced
below:
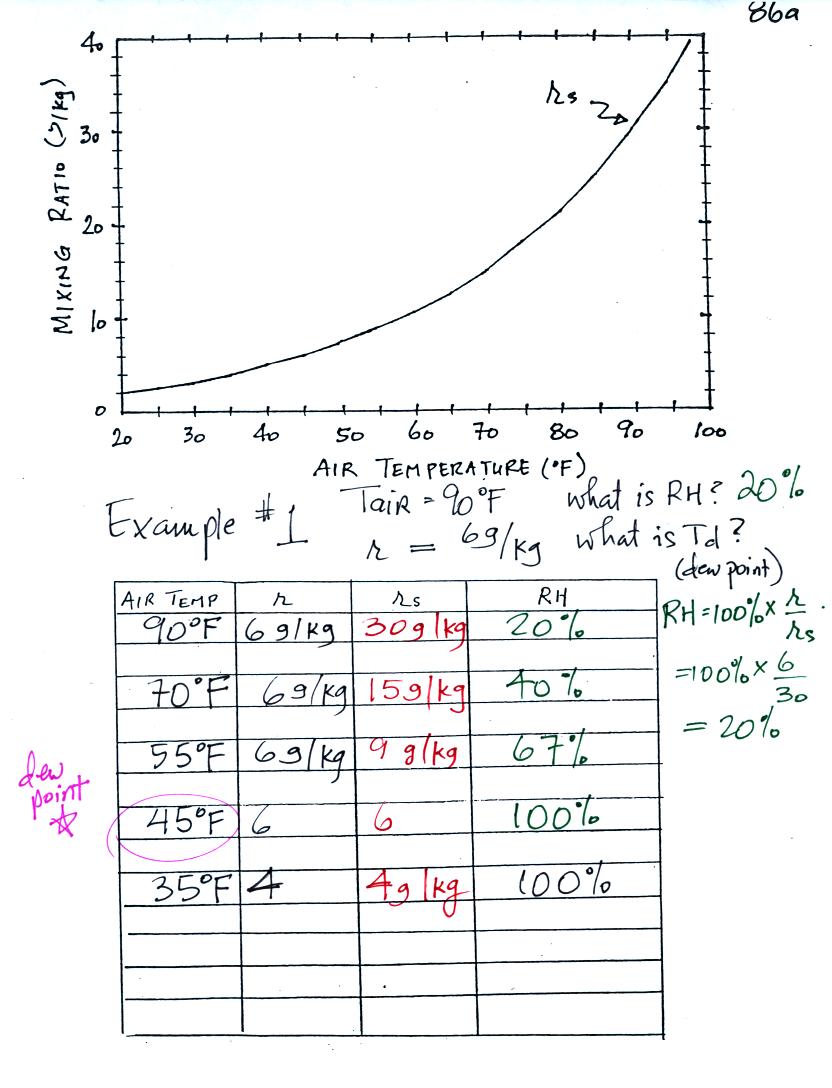
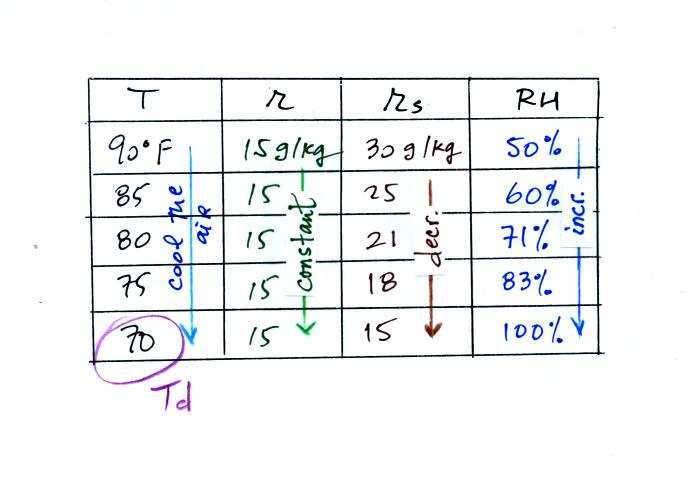
We're given an air temperature of 90 F and a mixing ratio
(r) of 6
g/kg.
We're supposed to find the relative humidity (RH) and
the dew point temperature.
We start by entering the data we were given in the
table. Once
you know the air's temperature you can look up the saturation mixing
ratio value; it is 30 g/kg for 90 F air. 90 F air could
potentially hold 30 grams of water vapor per kilogram of dry air (it
actually contains 6 grams per kilogram in this example). A table
of
saturation mixing ratio values can be found on p. 86 in the ClassNotes.
Once you know mixing ratio and saturation mixing ratio you can
calculate the relative humidity (you divide the mixing ratio by the
saturation mixing ratio, 6/30, and multiply the result by 100%).
You ought to be able to work out the ratio 6/30 in your head (6/30 =
1/5 = 0.2). The RH is 20%.
The numbers we just figured out are shown on the top line
above.
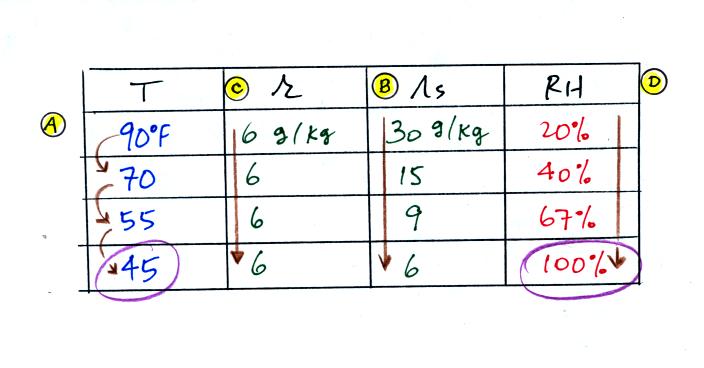
(A) We imagined cooling the air from 90F to 70F, then to 55F, and
finally to 45F.
(B) At each step we looked up the saturation mixing ratio and entered
it on the chart. Note that the saturation mixing ratio values
decrease as the air is
cooling.
(C) The mixing
ratio doesn't
change as we cool the air. The only
thing that changes r is adding or removing water vapor and we aren't
doing either.
(D) Note how the relative humidity is increasing as we cool
the
air. The air still contains the same amount of water
vapor it is
just that the air's capacity is decreasing.
Finally at 45 F the RH becomes 100%. This is kind of a special
point. You have cooled the air until it has become
saturated.
The dew point temperature in
this problem is 45 F.
What would happen if we cooled the air
further still, below the dew
point temperature?
35 F air can't hold the 6 grams of water vapor
that 45 F air can. You can only "fit" 4 grams of water vapor into
the 35 F air. The remaining 2 grams would condense. If
this happened at ground level the ground would get wet with dew.
If it happens above the ground, the water vapor condenses onto small
particles in the air and forms fog or a cloud. Now because water
vapor is being taken out of the air (and being turned into water), the
mixing
ratio will decrease from 6 to 4.
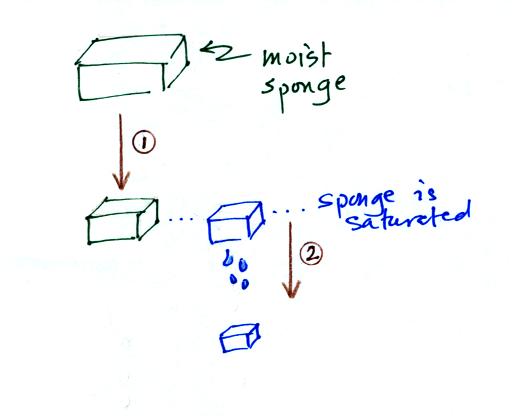
In many ways cooling moist air is liking squeezing a
moist sponge (I
don't think this
figure
was
shown
in class)
Squeezing the
sponge and reducing its volume is like cooling moist air and reducing
the saturation mixing ratio. At first when you sqeeze the sponge
nothing happens, no water drips out. Eventually you get to a
point where the sponge is saturated. This is like reaching the
dew point. If you squeeze the sponge any further (or cool air
below
the dew point) water will begin to drip out of the sponge (water vapor
will condense from the air).
Example 2
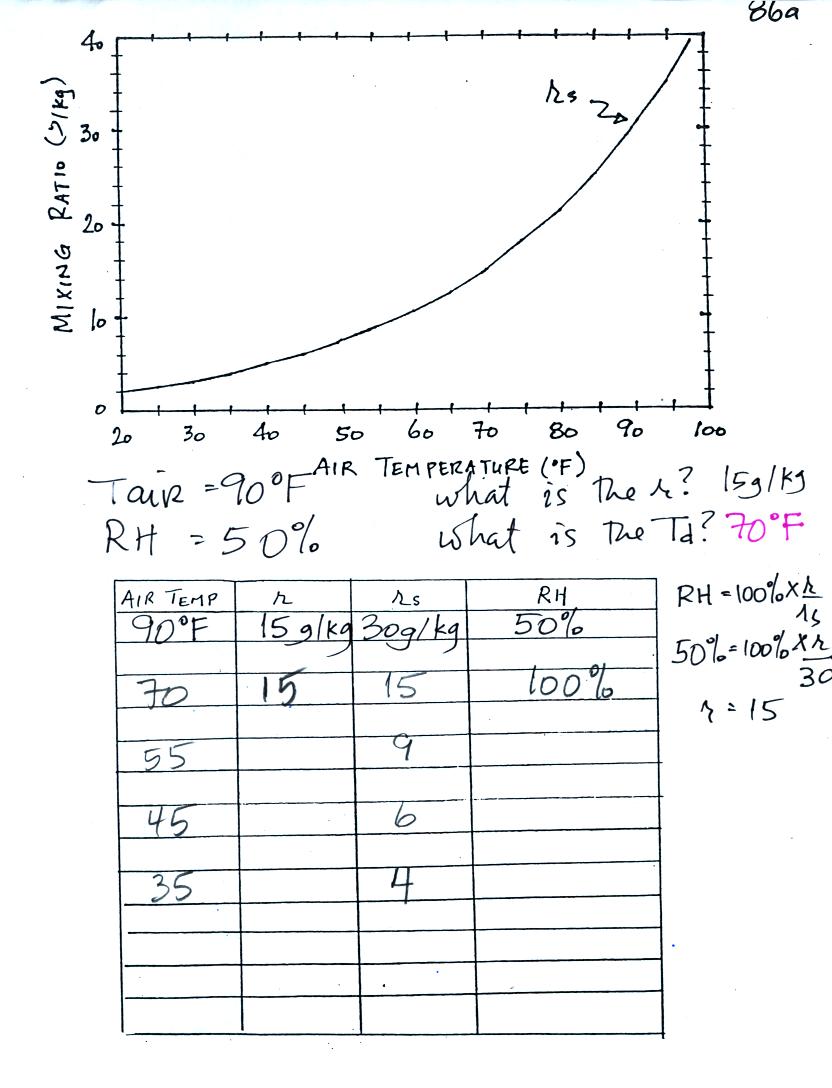
The work that we did in class is shown above. Given an air
temperature
of 90
F and a relative humidity of 50% you are supposed to figure out the
mixing ratio (15 g/kg) and the dew point temperature (70 F). The
problem is worked out in detail below:
First you fill in the air temperature and the RH data that
you are
given.
(A) since you know the air's temperature you can look up the
saturation mixing ratio (30 g/kg).
(B) Then you might be able to figure out the mixing ratio in your
head. Air that is filled to 50% of its capacity could hold up to
30 g/kg. Half of 30 is 15, that is the mixing ratio. Or you
can substitute into
the relative humidity formula and solve for the mixing ratio.
Finally you imagine cooling the air. The
saturation mixing ratio decreases, the mixing ratio stays constant,
and the relative humidity increases. In this example the RH
reached 100% when the air had cooled to 70 F. That is the dew
point temperature.
We can use
results from humidity problems #1 and #2 worked in class on Monday to
learn a useful rule.
In the first
example the difference between the air and dew point
temperatures was large (45 F) and the RH was low (20%).
In
the
2nd problem the difference between the air and dew point
temperatures was
smaller (20 F) and the RH was higher (50%). The easiest way to
remember
this
rule is to remember the case where there is no difference between the
air and dew
point temperatures. The RH then would be 100%.
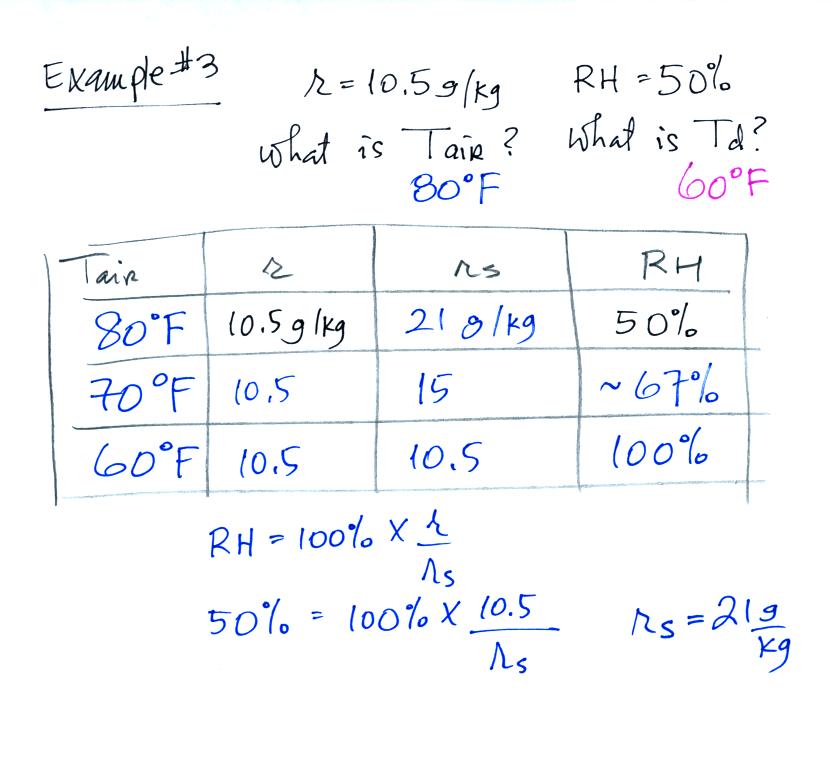
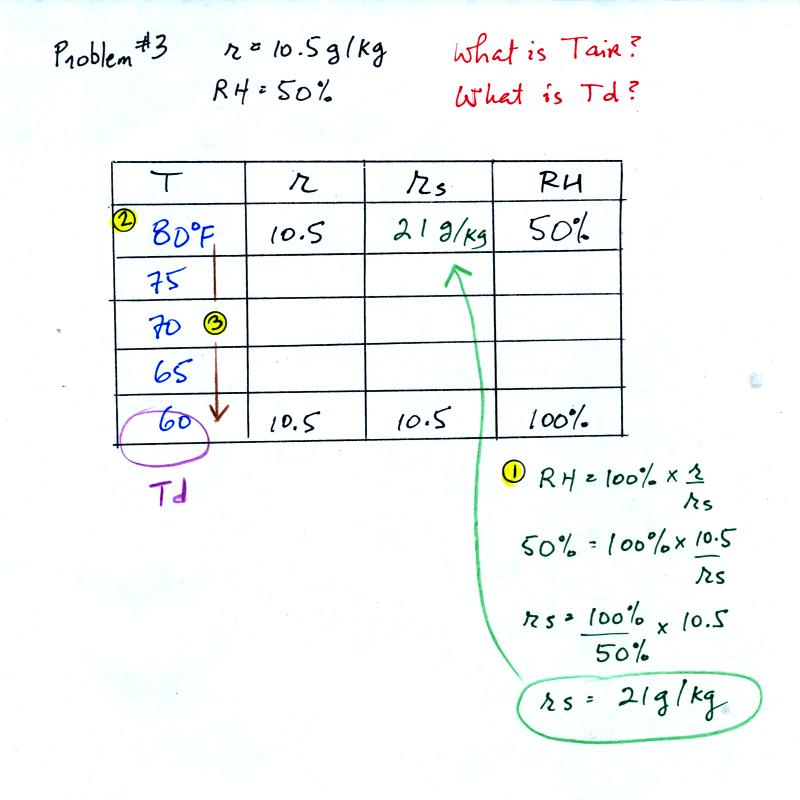
Example 3
You're given the mixing ratio (10.5) and the relative humidity
(50). What are the units (g/kg and %). Here's the play by
play solution to the question
You are given a
mixing ratio
of 10.5 g/kg and a relative humidity of 50%. You need to figure
out the air temperature and the dew point temperature.
(1) The air contains 10.5 g/kg of water vapor, this is 50%,
half, of what the air
could potentially hold. So the air's capacity, the saturation
mixing ratio must be 21 g/kg (you can either do this in your head or
use the RH equation following the steps shown).
(2) Once you know the saturation mixing
ratio you can look up the air temperature in a table (80 F air has a
saturation mixing ratio of 21)
(3) Then you
imagine cooling the air until the RH becomes 100%. This occurs at
60 F. The dew point is 60 F.
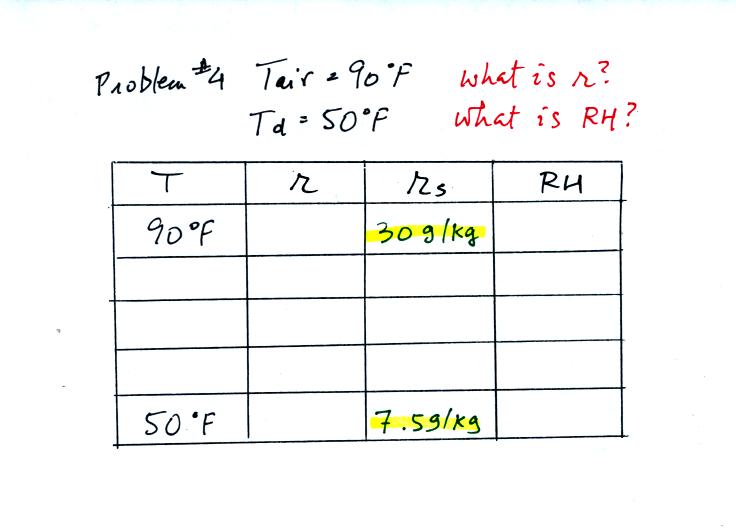
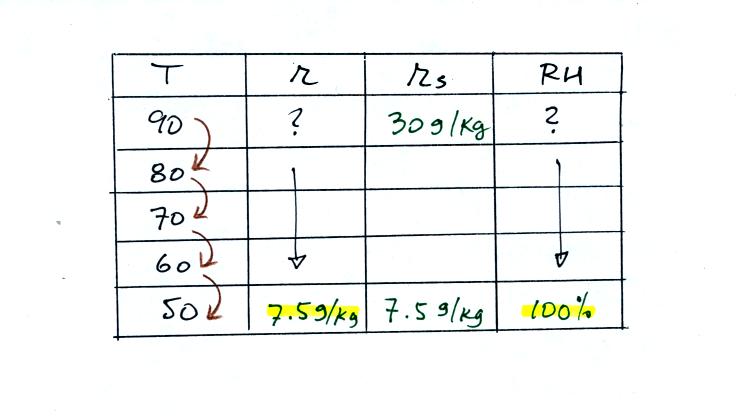
Example 4
probably the most difficult problem of the bunch.
Here's what we did in class, we
were given the air temperature and the dew point temperature. We
were supposed to figure out the mixing ratio and the relative
humidity.
We enter the two temperatures onto a chart and look up the
saturation
mixing ratio for each.
We ignore the fact that we don't know the mixing
ratio. We do know that if we cool the 90 F air to 50 F the RH
will
become
100%. We can set the mixing ratio equal to the value of the
saturation mixing ratio at 50 F, 7.5 g/kg.
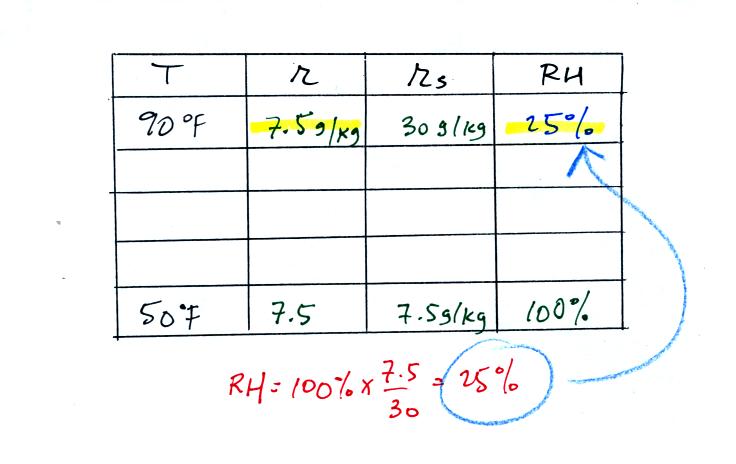
Remember back to the three earlier examples. When we
cooled air
to the the dew point, the mixing ratio didn't change. So the
mixing ratio must have been 7.5 all along. Once we know the
mixing ratio in the 90 F air it is a simple matter to calculate the
relative humidity, 25%.
Here's a list of some of the important facts and properties of the
4 humidity variables that we have been talking about. This list wasn't
shown in class.