ATMO/ECE 489/589  Final Exam
May 8, 2015

Everyone should answer Question #1 (25 pts)
ATMO/ECE 489 students should then answer 3 of the remaining 6 questions (20 pts each)
ATMO/ECE 589 students should answer any 4 of the remaining questions (20 pts each)

1.
Please answer any 5 of the following short answer questions

(a)    What two parameters of the lightning return stroke current waveform are responsible for producing high voltages on a grounded down conductor connected to a lightning rod?  Give typical values for these two parameters.

(b)    A cloud-to-ground discharge has a duration that is usually less than 1 second.  Why does the thunder last much longer than that?

(c)    Explain how the Optical Transient Detector and the Lightning Imaging Sensor on satellites are able to detect lightning optical signals during the day against the very bright background of sunlight reflected by the top of the thunderstorm cloud.

(d)    Explain why a series of lightning rods installed on the roof of a building might adequately protect against high current amplitude return strokes but not against the lower current amplitude strokes.

(e)    Why would two down conductors in the lightning protection system sketched below be preferable to just a single down conductor?



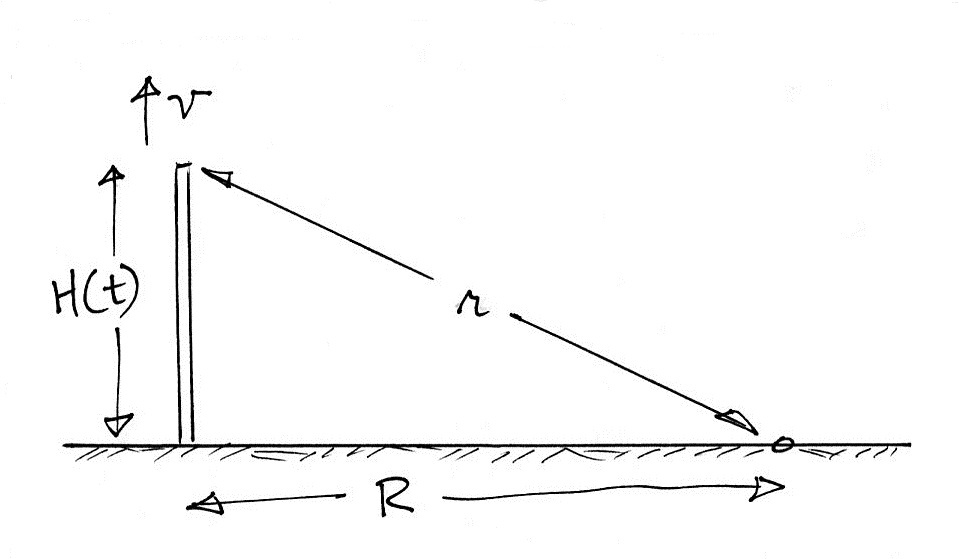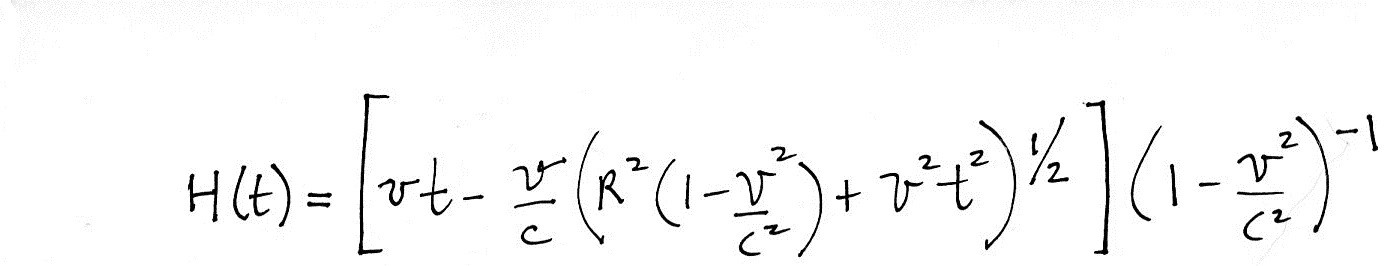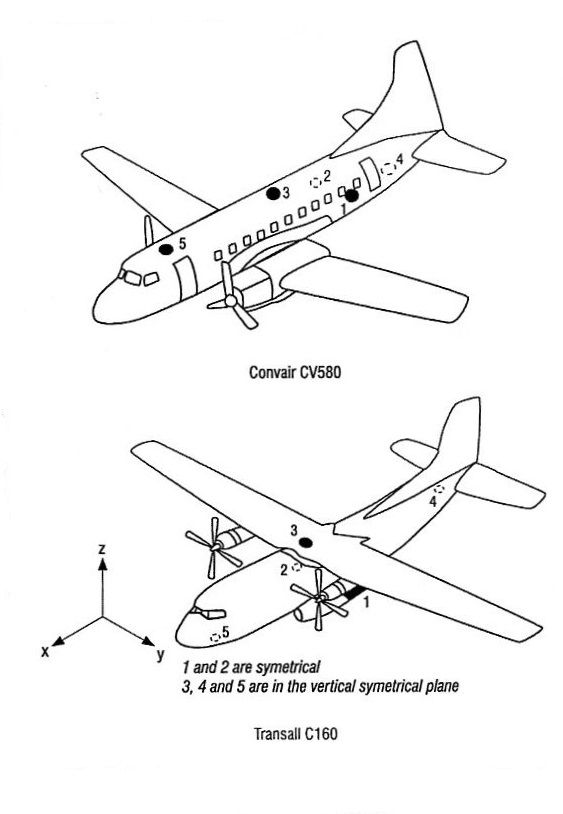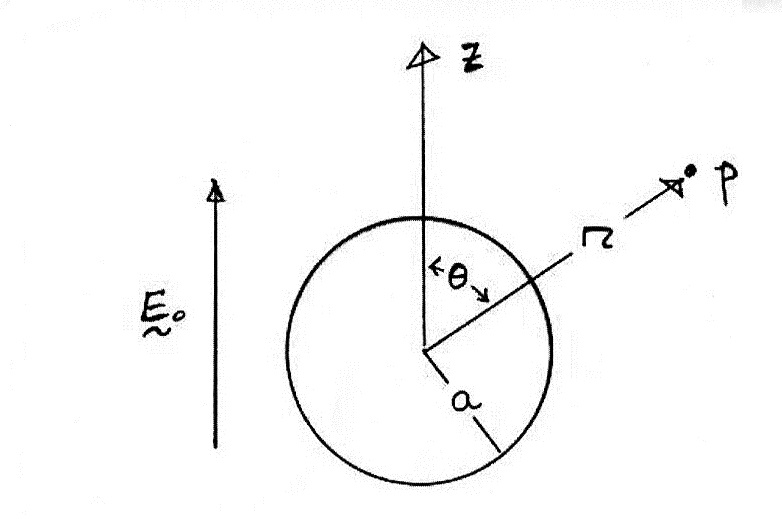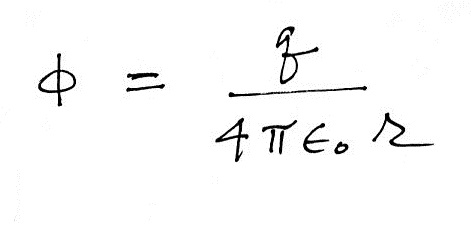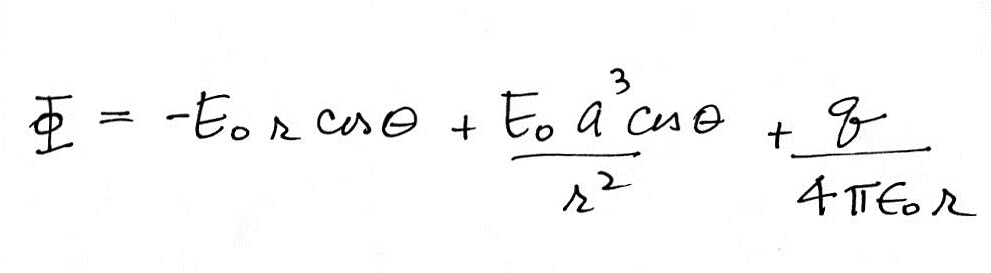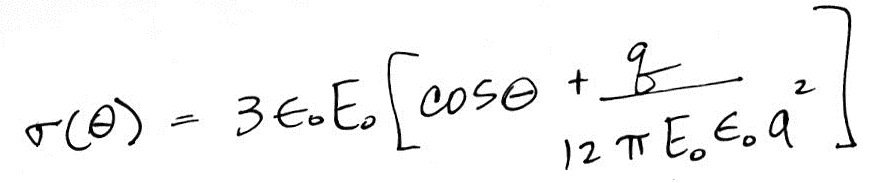
(f)    What do you think is the simplest and most effective way of protecting sensitive home electronics from damage during a lightning storm?

(g)    A two station network of magnetic direction finders would not do a very good job locating lighting that strikes on the baseline between the two stations.  Why is this?  What two ways are there that the magnetic direction finder data could be used to improve the accuracy of locations on the baseline.

(h)    Where are the highest lightning flash densities found in the world?  Is there more lightning over the land or over the ocean?  When during the year does the peak lightning activity occur?

(i)    Describe the sequence of events that occur during a rocket triggered lightning discharge.  In what way(s) is a triggered discharge different from a natural cloud-to-ground discharge?  In what way(s) are the two kinds of discharges similar?

(j)    Describe how lightning return stroke currents can be measured directly and remotely.

2.




Assume that a return stroke is propagating upward at a constant speed v.  Show that the height of the visible channel, H(t), that an observer a distance R away would see at time t is



This is Eqn. (3) in Guo and Krider (1982).

3.
In our Friday April 3 class we looked at some of the characteristics of lightning striking aircraft.  Many of the aircraft in those research studies made measurements of the thunderstorm electric fields.  In particular, they wanted to determine what field amplitudes were needed for an aircraft to initiate lightning.  Field mills were mounted at multiple locations on the aircraft body and a complex analysis procedure was used to determine the 3-dimensional field surrounding the aircraft and also to account for any charge that might have built up on the aircraft.  The locations of 5 field mills on the Convair CV580 and the Transall C160 are shown below

This question will make use of a much simpler geometry, a conducting sphere, and will assume the sphere is placed in a uniform, vertically oriented, ambient electric field (the aircraft studies generally assume that the field is uniform but of unknown orientation).

In our January 30 lecture we derived the potential function, Φ(r,θ) in the space surrounding the sphere


The problem geometry is shown above.  The potential function that we ended up with is shown below


One of the boundary conditions that we used when working out the problem was that the potential was constant on the surface of the sphere, that is the case above when r = a.  Now we will imagine that the sphere is charged.  The potential function for a point charge is

We'll add this expression to the equation above for the uncharged sphere (here's a reference that convinced me this is a valid approach)

(the Φo term was dropped in this expression).  Note that Φ is constant on the surface of the sphere in this case also (r = a in the expression above).

The Final Exam question has three parts:

(a)  The charge on the sphere is clearly not positioned at the center of the sphere.  Rather it is spread out over the surface of the sphere.  Using the expression above show that the surface charge density on the surface of the sphere is


(b) Integrate this expression for surface charge density over the surface of the sphere

(c) Imagine you were able to measure the electric field at the top and bottom surfaces of the sphere (just as field mills are able to measure the electric field at various locations on an aircraft).  Show how you could use the measurements of Etop and Ebottom to determine both the ambient field, Eo, and the charge on the conducting sphere, q.

4.
On April 26, 1986, an accident at the Chernobyl nuclear reactor sent a plume of radioactive cesium (137Cs), iodine (131I), and ruthenium (103Ru) into the lower atmosphere that was subsequently carried to many locations in Europe in a few days.  The plume arrived over Greece on May 3.  The figure below compares the long term average daily variation of positive conductivity λ+ observed in May (dotted line) with enhanced conductivity observed in May 1986 (solid line).  (figure adapted from D. REtalis and A. Pitta, "Effects on Electrical Parameters at Athens Greece by Radioactive Fallout from a Nuclear Power Plant Accident," J. Geophys. Res., 94, 13093-13097, 1989)



The exam question has 3 parts:
(a)   Would you have expected the higher conductivity in May 1986 to have increased or decreased the strength of the fair weather electric field at the ground? 

(b)   Use the positive conductivity values in the figure above to determine the positive small ion concentrations, n+, before and after the arrival of the radioactive plume.

(c)  Assuming steady state conditions and neglecting small ion to particle attachment, determine the small ion production rate, q, before and after the arrival of the plume.  You may assume the numbers of positive and negative small ions are equal.

The charge on an electron is 1.6 x 10-19 C, you may used the values given for 0 km altitude on the "Summary of Electric Parameters vs Altitude" handout for any other constants that you might need.

5.
Assume that there are N strikes per kilometer per year to a long power line.  What is the probability that the nearest strike is between x and x + dx.  Basically you are being asked to derive a one-dimensional version of the nearest neighbor probability density function.  You can assume that the point of reference is on the left end of the line (0 in the sketch below) and that the line extends to the right without limit.


6.
Assume that a cloud-to-ground discharge occurs 250 km from one of the sensors in the National Lightning Detection Network.  Before being used to estimate the peak currents for the strokes in the discharge, the measured peak B field amplitudes would be range normalized to 100 km and a correction for attenuation of the signal by propagation would be made.  Discuss how these are both done.  What relation would then be used to determine the peak current values?

7.
The sensors in the National Lightning Detection Network use measurements of the two perpendicular components of the horizontal magnetic field radiated by a lightning discharge to determine a bearing angle to the strike point.  The location of a strike could then be determined by finding the intersection of vectors from as few as two stations (accuracy is better when vectors from multiple stations are used). 

The NLDN sensors also measure the time of arrival (TOA) of the lightning signal at each sensor.  TOA data serve as an additional, independent, way of locating a lightning discharge.  In this case a single TOA difference measurement, Δt, for a pair of stations isn't enough to locate a strike.  All you can say for a single TOA difference is that the strike point was located somewhere on a hyperbola.  This is in fact the definition of a hyperbola: "the set of points in a plane whose distance to fixed points in the plane have a constant difference."  The object of this problem is to demonstrate the validity of that statement.

We'll consider the geometry shown below.  Sensors are located a Points 1 & 2 located at (-c, 0) and (+c, 0).  The hyperbola crosses the x-axis at x = a.  Point
(x, y) is just an arbitrary point on the hyperbola and is a distance d1 from Point 1 and a distance d2 from Point 2.  The values of  d1  and d2 will change depending on x and y but the difference d1- d2 will remain the same for any point on the hyperbola.





The problem has three parts:
(a)  Show that d1- d2= 2a  (hint: since d1- d2  remains constant, you can choose any point on the hyperbola to determine d1- d2 )
(b)  Demonstrate that the expression above after some manipulation leads to



(c)  Show that at large values of x and y the hyperbola becomes a straight line