Friday Jan. 30, 2009
click here to download today's notes in a more printer friendly format.

Vampire Weekend supplied what I thought was an appropriate song (M79) for the start of what looks to be a glorious weekend.

Next week's reviews (for the Practice Quiz) will both be held in FCS 225 from 4-5 pm on Monday and Tuesday afternoon.
So far this semester we have learned about the composition of the atmosphere and about some of the main air pollutants.  Today we will start looking at how atmospheric characteristics such as air temperature, air pressure, and air density change with altitude.  In the case of air pressure we first need to understand what pressure is and how it changes as you move vertically through the atmosphere.

An iron bar was passed around at the beginning of class.  You were supposed to guess how much it weighed.



We'll come back to this later in the period.

A pair of bottles, one containing water and the other an equal volume of mercury, were also passed around in class. Feel the difference in the weights of the two bottles.  Mercury is much denser than water.

Some of you may have seen Venus and the crescent moon in Thursday's evening sky - it was quite spectacular.  The sight motivated me to try to write a tanka poem.  Haiku poems have 3 lines, a tanka poem has 5 lines (with 5, 7, 5, 7, and 7 syllables per line as you move from top to bottom).  Here is what I had come up with so far:


I asked for some help coming up with the last line (sorry no extra credit this time) while I was occupied handing out the bar and the bottles.



Before we can learn about atmospheric pressure, we need to review the terms mass and weight.  In some textbooks you'll find mass defined as "amount of stuff" or "amount of a particular material."  Other books will define mass as inertia or as resistance to change in motion (this comes from Newton's 2nd law of motion, we'll cover that later in the semester).  The next picture illustrates both these definitions.  A Cadillac and a volkswagen have both stalled in an intersection.  Both cars are made of steel.  The Cadillac is larger and has more steel, more stuff, more mass.  The Cadillac is also much harder to get moving than the VW, it has a larger inertia (it would also be harder to slow down once it is moving).


It is possible to have two objects with the same volume but very different masses.  The bottles of water and mercury that were passed around class were an example (thanks for being so careful with the mercury).

Weight is a force and depends on both the mass of an object and the strength of gravity.  We tend to use weight and mass interchangeably because we spend all our lives on earth where gravity never changes.



Any three objects that all have the same mass (even if they had different volumes and were made of different materials) would necessarily have the same weight. Conversely:

Three objects with the same weight would also have the same mass.

The difference between mass and weight is clearer (perhaps) if you compare the situation on the earth and on the moon.

If you carry an object from the earth to the moon, the mass remains the same (it's the same object, the same amount of stuff) but the weight changes because gravity on the moon is weaker than on the earth.


In the first example there is more mass (more dots) in the right box than in the left box.  Since the two volumes are equal the box at right has higher density.  Equal masses are squeezed into different volumes in the bottom example.  The box with smaller volume has higher density.


The air that surrounds the earth has mass.  Gravity pulls downward on the atmosphere giving it weight.  Galileo conducted (in the 1600s) a simple experiment to prove that air has weight. 

Pressure is defined as force divided by area.  Air pressure is the weight of the atmosphere overhead divided by the area the air is resting on.  Atmospheric pressure is determined by and tells you something about the weight of the air overhead.

Under normal conditions a 1 inch by 1 inch column of air stretching from sea level to the top of the atmosphere will weigh 14.7 pounds.  Normal atmospheric pressure at sea level is 14.7 pounds per square inch (psi, the units you use when you fill up your car or bike tires with air).



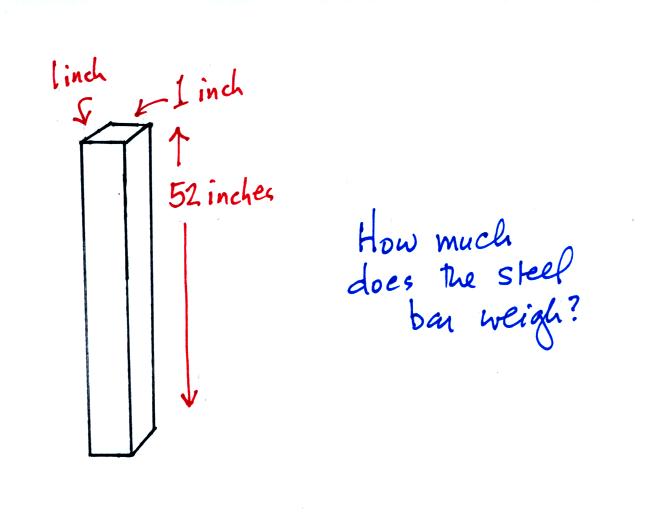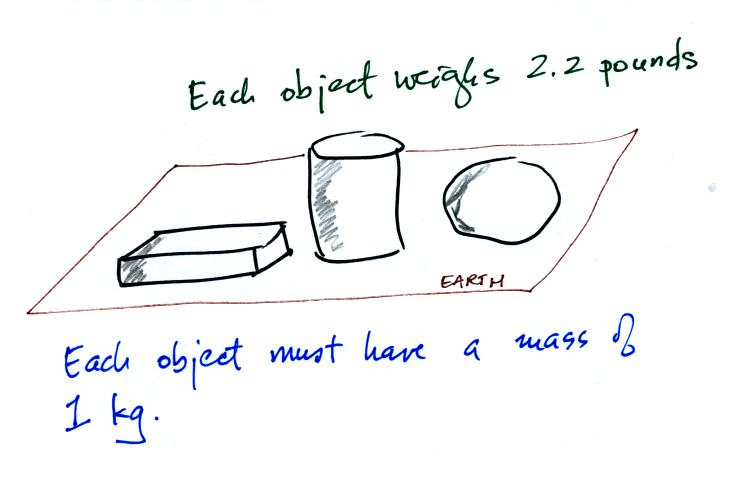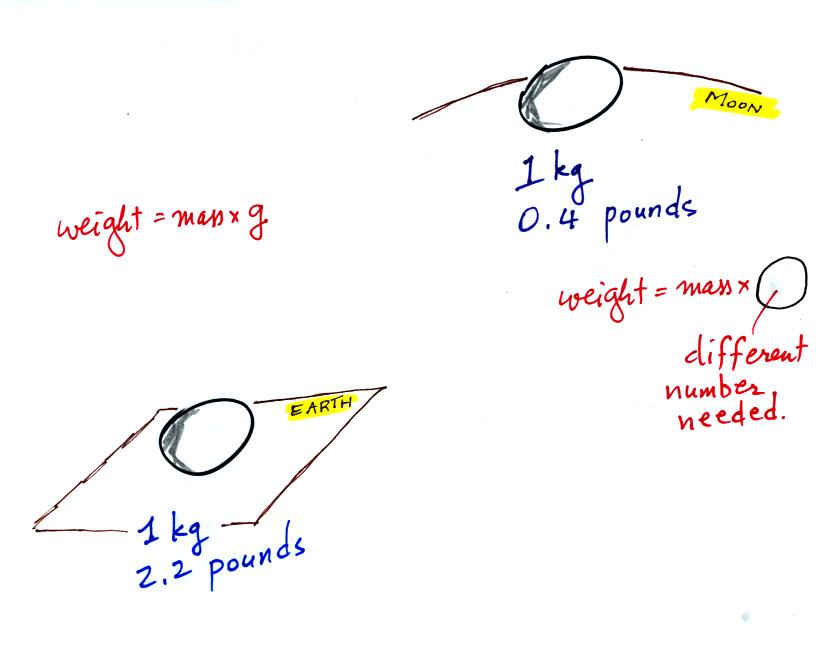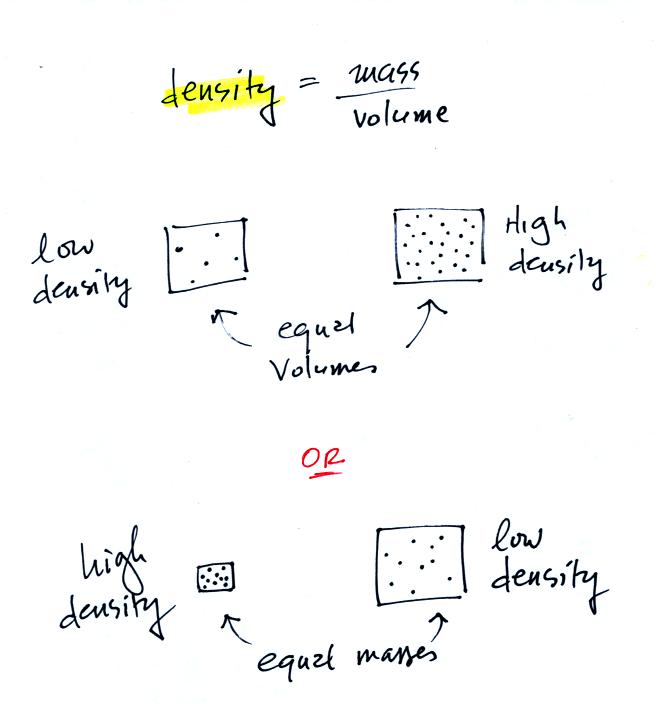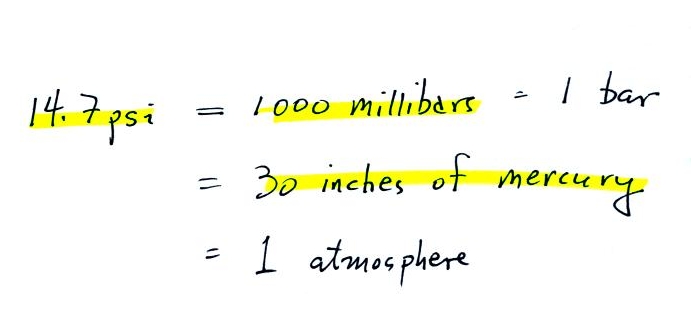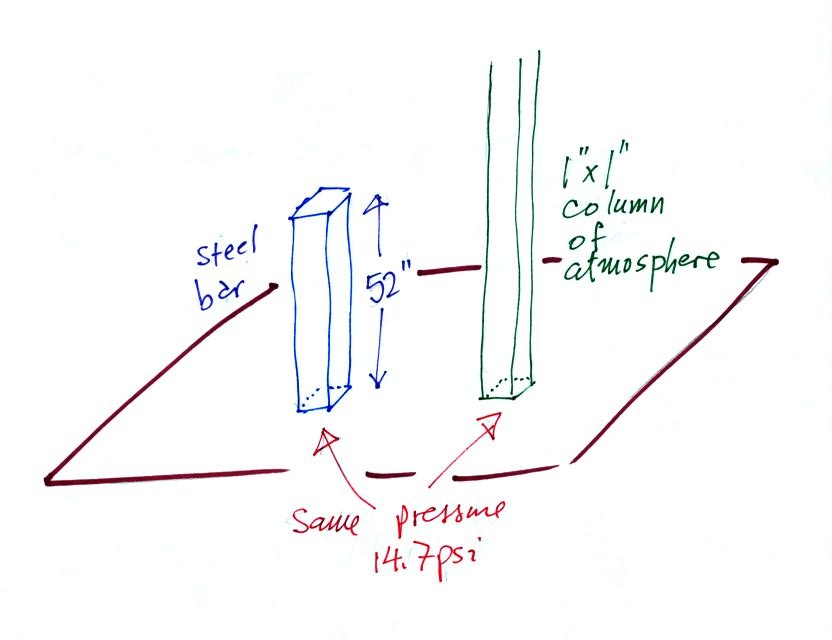
Now here's where the steel bar comes in.  The steel bar also weighs exactly 14.7 pounds (many people thought it was heavier than that).  Steel is a lot denser than air, so a steel bar only needs to be 52 inches tall to have the same weight as an air column that is 100 miles or more tall.

Here are some of the other commonly used pressure units. 


Typical sea level pressure is 14.7 psi or about 1000 millibars (the units used by meterologists and the units that we will use in this class most of the time) or about 30 inches of mercury (refers to the reading on a mercury barometer).  If you ever find yourself in France needing to fill your automobile tires with air (I lived in France for a while and owned a  Peugeot 404) remember that the air compressor scale is probably calibrated in bars.  2 bars of pressure would be equivalent to 30 psi.

The word "bar" basically means pressure and is used in a lot of meteorological terms (the figure above wasn't shown in class).
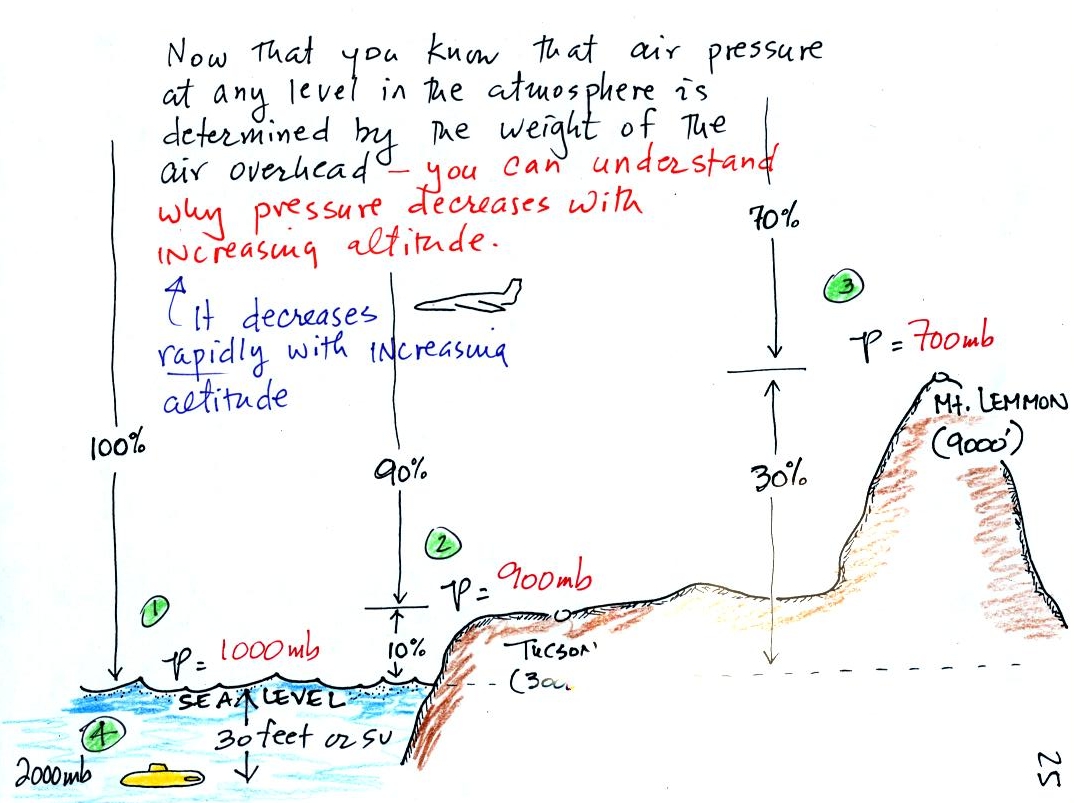
Pressure at sea level is determined by the weight of the air overhead.  What about pressure at some level above sea level?
We can use a stack of bricks to try to answer this question. 


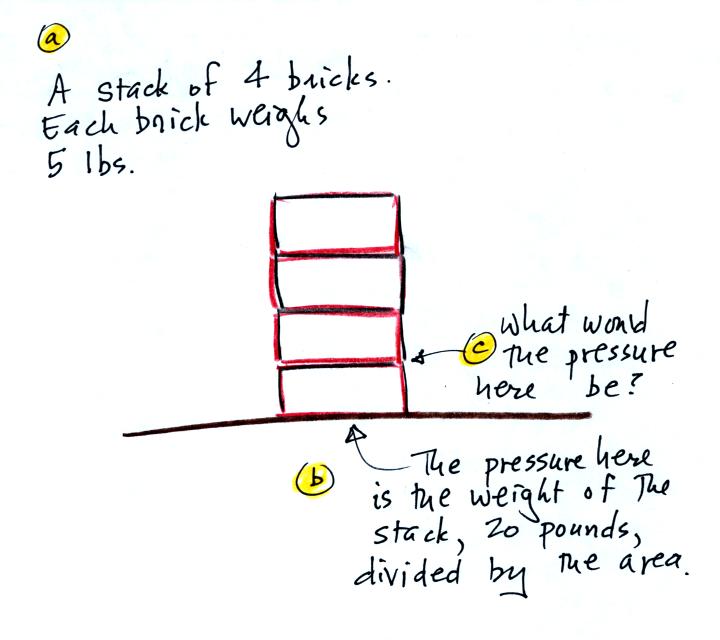
Each brick weighs 5 pounds.  At the bottom of the 4 brick tall pile you would measure a weight of 20 pounds.  If you moved up a brick you would measure a weight of 15 pounds, the weight of the three bricks still above.  To get the pressure you would need to divide by the area.  It should be clear that weight and pressure will decrease as you move up the pile.

In the atmosphere, pressure at any level is determined by the weight of the air still overhead.  Pressure decreases with increasing altitude because there is less and less air remaining overhead.  The numbered points on the figure below were added after class.


At sea level altitude, at Point 1, the pressure is normally about 1000 mb.  That is determined by the weight of all (100%) of the air in the atmosphere.

Some parts of Tucson, at Point 2, are 3000 feet above sea level (most of the valley is a little lower than that).  At 3000 ft. about 10% of the air is below, 90% is still overhead.  It is the weight of the 90% that is still above that determines the atmospheric pressure in Tucson.  If 100% of the atmosphere produces a pressure of 1000 mb, then 90% will produce a pressure of 900 mb. 

Pressure is typically about 700 mb at the summit of Mt. Lemmon (9000 ft. altitude at Point 3) and 70% of the atmosphere is overhead..

Pressure decreases rapidly with increasing altitude.  We will find that pressure changes more slowly if you move horizontally.  It is small horizontal changes that cause the wind to blow however.

Point 4 shows a submarine at a depth of about 33 ft.  The pressure there is determined by the weight of the air and the weight of the water overhead.  Water is much denser and much heavier than air.  At 33 ft., the pressure is already twice what it would be at the surface of the ocean (2000 mb instead of 1000 mb).

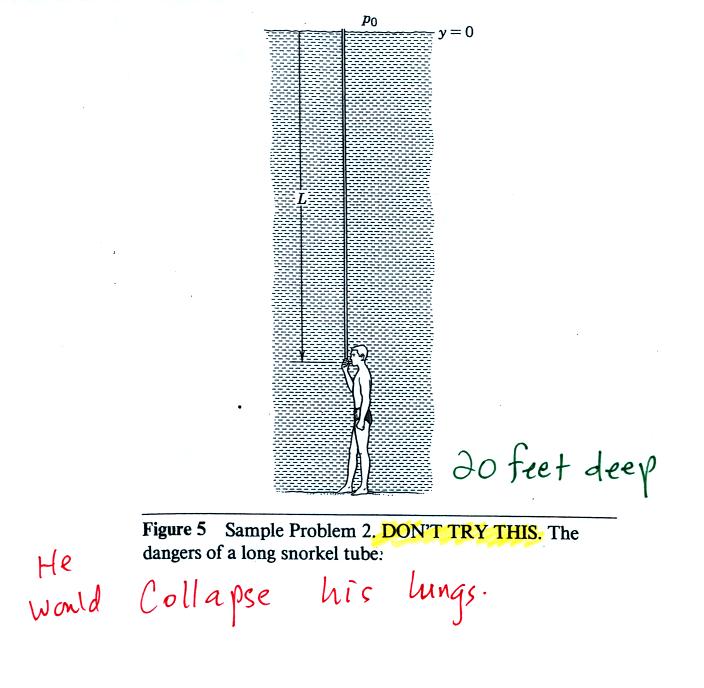
The person in the picture below (from a Physics textbook) is 20 feet underwater.  At that depth there is a pretty large pressure pushing against his body from the surrounding water.  The top of the snorkel is exposed to the much lower air pressure at the top of the pool.  If the swimmer puts his mouth on the snorkel the pressure at the bottom of the pull would collapse his lungs.



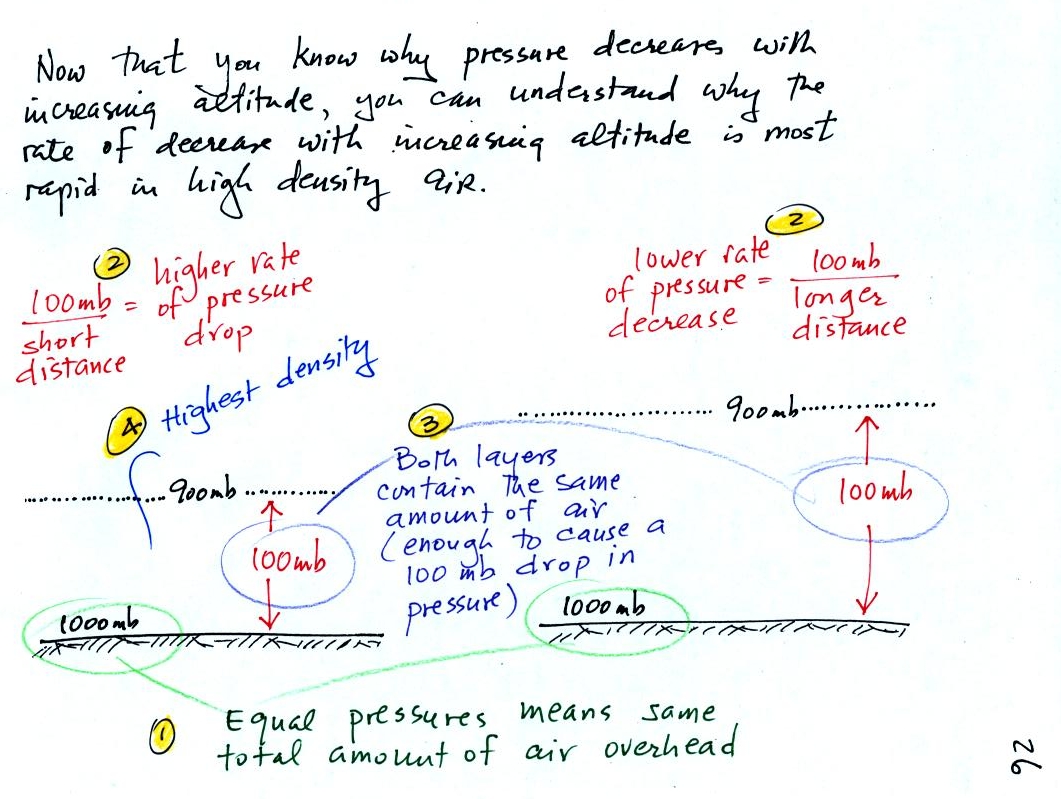
There is a lot going on in this picture.  1000 mb at Point 1  is a typical value for sea level pressure.  The fact that the pressures are equal at the bottoms of both sides of the picture means that the weight of the atmosphere at the bottom of the picture on the left is the same as the weight of the atmosphere at the bottom of the picture at right.  The only way this can be true is if there is the same total amount (mass) of air in both cases.

Point 2 - Moving upward from the ground we find that pressure decreases to 900 mb at the level of the dotted line in the picture at left.  This is what you expect, pressure decreases with increasing altitude.  In the figure at right you need to go a little bit higher for the same 100 mb decrease.

The most rapid rate of pressure decrease with increasing altitude is occurring in the picture at left because the 100 mb change occurs in a shorter distance.

Point 3 - Since there is a 100 mb drop in both the layer at left and in the layer at right, both layers must contain the same amount (mass) of air.

Point 4 - The air in the picture at left is squeezed into a thinner layer than in the picture at right.  The air density in the left layer is higher than in the layer at right.

By carefully analyzing this figure we have proved to ourselves that the rate of pressure decrease with altitude is higher in dense air than in lower density air.

This is a fairly subtle but important concept.  This concept will come up 2 or 3 more times later in the semester.  For example, this concept partly explains why hurricanes can intensify and get as strong as they do.