Monday Feb. 12, 2007
Photocopies of the Quiz #1 Study Guide
and answers to the most recent optional
assignment were distributed in class. Both are also available
online. Remember that Quiz #1 this Wednesday will also cover
material on the Practice Quiz Study Guide.
The
semester is about 1 month old and we have managed to finish Chapter 1
in the textbook. It is time to move on to Chapter 2.
Here is a brief introduction (found on pps 43-44 in the photocopied
Class Notes) to the some of the things we will cover in
Chapter 2; we may run into a lot of confusing concepts and details in
Chapter 2 and may lose sight of our overall objectives.
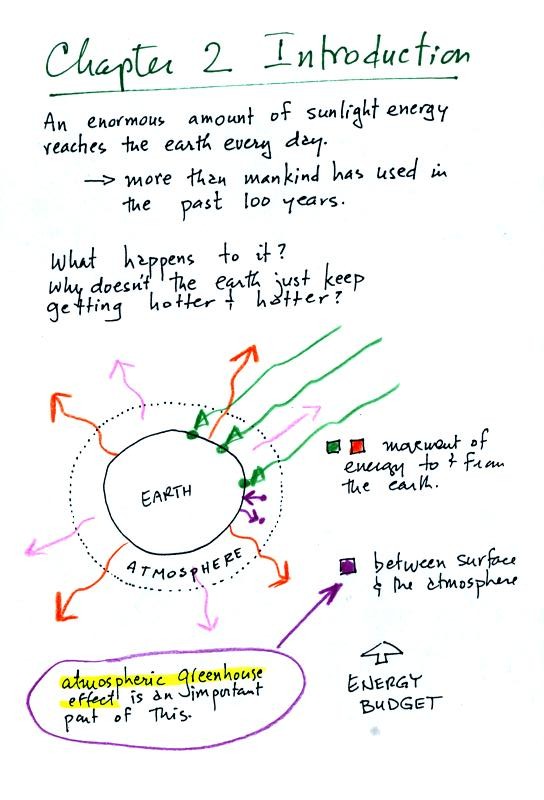
An enormous amount of sunlight energy reaches the earth
everyday (the green arrows in the figure above).
We will learn how it is possible for this form of energy to travel
through empty space. We are aware of this sunlight energy because
we can see it (at least some of it) and we can feel it (you get warm
when you
stand in the sunlight). With all of this energy arriving at and
being
absorbed by the earth, what keeps the earth from getting hotter and
hotter? The answer is that the earth also sends energy back into
space (the orange and pink arrows in the figure, travelling from the
earth and the atmosphere into space). This infrared light is an
invisible form of energy; we
don't usually feel it either). A balance
between incoming and outgoing energy is achieved and the earth's annual
average temperature remains constant.
We will also look closely at energy transport between the earth's
surface and the atmosphere. That is where the atmospheric
greenhouse operates. That will be a major goal in Chapter 2 - to
understand the atmospheric greenhouse effect.
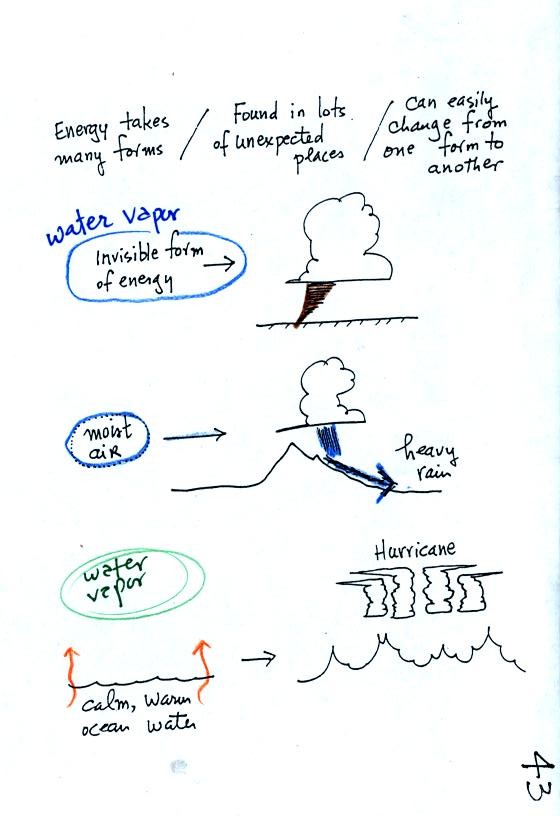
Water vapor is a particularly important form of invisible
energy.
When water vapor condenses to produce the water droplets (or ice
crystals) in a
cloud, an enormous amount of energy is released into the atmosphere.
It is hard to visualize or appreciate energy released into the
atmosphere during condensation. You can imagine the work that you
would do carrying a gallon of water
(8 pounds) from Tucson to the top of Mt. Lemmon. To
accomplish
the same thing Mother Nature must first evaporate the water and (if my
calculations are correct) that requires about 100 times the energy that
you would use to carry the 8 pounds of water to the summit of Mt.
Lemmon. And Mother Nature transports a lot more than just a
single gallon.

Kinetic energy is energy of motion. Latent heat energy
is an unappreciated form of energy.
The four energy transport
processes are listed at the bottom of the page above. By far the
most important process is electromagnetic radiation (light is a common
form of electromagnetic radiation). This is the
only process that can transport energy through empty space.
Electromagnetic radiation is also responsible for about 80% of the
energy transport between the ground and atmosphere. You might be
surprised to learn that latent heat is the second most important
transport process.

One of the main objectives in Chapter 2 is to understand the
greenhouse
effect.
I've taken
the information on p. 45 in the photocopied notes and split it into two
parts.
When you add energy to an object, the object will usually warm
up. Below we work out the equation that connects energy added and
the resulting temperature change. The equation can also be used
when energy is removed from an object. In that case the object
will cool.

When you add energy to something the temperature change will
depend on
how much energy was added. So delta E is in the numerator of the
equation. When you add equal amounts of energy to a small pan of
water and to a large pan of water, the small pan will heat up more
quickly. The temperature change, delta T, will depend on the
mass. A large mass will mean a small delta T, so mass should go
in the denominator of the equation. Different materials
react differently when energy is added to them. A material with a
large specific heat will warm more slowly than a material with a small
specific heat. Specific heat behaves in the same kind of way as
mass. Specific heat is sometimes called "thermal mass."
An object will usually warm when you add energy to it. But there
is another possibility (mentioned at the bottom of the figure).
The object could change phase. Adding energy to ice might cause
the
ice to melt. Adding energy to liquid nitrogen could cause the
nitrogen to
evaporate and turn into nitrogen gas.

Here's an example that shows the effect of specific
heat. Equal
amounts of energy (note that calories are units of energy) are added to
equal amounts of water and dirt. We use water and dirt in the
example because most of the earth's surface is either water or dirt.
Water has a higher specific heat than soil, it only warms up 5 C.
The soil warms up 20 C.
We did a
short experiment in class. The object of the experiment was to
measure the latent heat of
vaporization of liquid nitrogen. That just means measuring the
amount of energy needed to evaporate a gram of liquid nitrogen.
The students that are doing Experiment #2 are measuring the latent heat
of fusion of ice, the energy needed to melt one gram of ice.
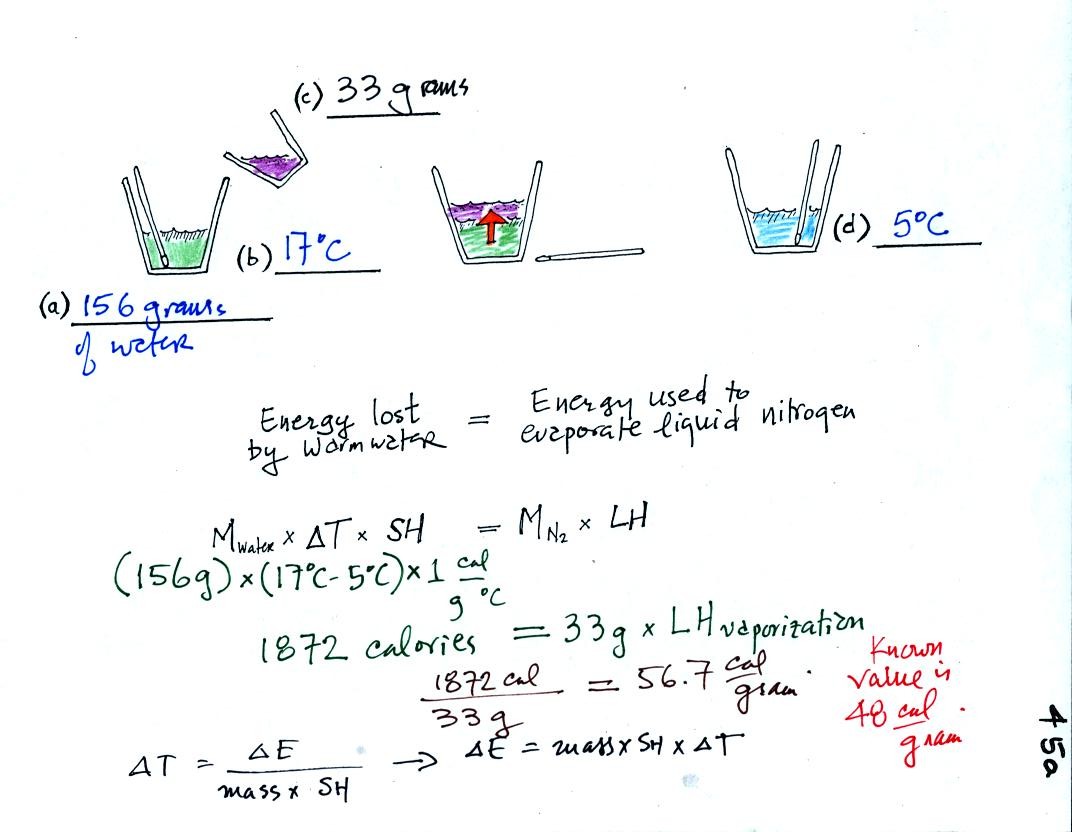
First we will make use of the Delta T vs Delta E equation
(see lower left corner in the picture above). Rather than solving
for Delta T we will
rearrange the equation and solve for Delta E.
We poured 156 grams of water into a styrofoam cup and measured its
temperature (17 C). Then we weighed out 33 grams of liquid
nitrogen into a second cup and poured it into the cup of water (after
having removed the thermometer). We waited until all the liquid
nitrogen had evaporated and remeasured the temperature of the water.
It takes energy to turn liquid nitrogen into gaseous nitrogen.
The needed energy came from the water. When energy is removed
from the water the water cools (to 5 C). By measuring how much
the water
cooled and knowing how much water we had we can calculate how much
energy was given up by the water. That is the 1872 calorie
figure above. This was used to evaporate 33 grams of liquid
nitrogen. So 56.7 calories was needed per gram. That is our
measured value. The know value is 48 cal/g, so our measurement
was reasonably close to the known value (the experiment worked a little
better in the Tuesday morning class, we measured 52.5 calories/gram.






