Tuesday Oct. 18, 2016
Zaz "Je
Veux" (3:35) "Si jamais
j'oublie" (3:26), Zaz & Pablo Alboran "Sous
le Ciel de Paris" (3:15), Zaz a Montmartre "Les
Passants" (4:20),
Kids United "On Ecrit
Sur Les Murs" (2:59), Kids United with Black M "Sur Ma
Route" (4:10)
All but about 15 of the quizzes have been graded and were
returned today. I'll have the remaining quizzes on
Thursday. Between now and then, I'll try to get
all the Quiz #2 scores online so that you can see how you did.
An In-class
Optional Assignment was handed out in class today.
If you download the assignment and turn it in at the beginning
of class on Thursday you can receive at least partial credit.
We're making good progress on the Expt. #2 reports. I
should have them ready to be returned on Thursday.
Between now and the next quiz
humidity variables - ways of measuring and
tracking the amount of moisture in the air.
cloud formation, naming and identifying clouds,
satellite photographs of clouds (probably a 1S1P topic)
formation of precipitation, types of
precipitation
Today: humidity variables
Humidity = moisture
(water vapor) in the air.
This
topic and the terms that we will be learning are probably
new and might be confusing. So here's an
introduction. We will be mainly be
interested in 4 variables:
Your task will be to learn the
"jobs" of these variables, their units, and what can cause them
to change value.
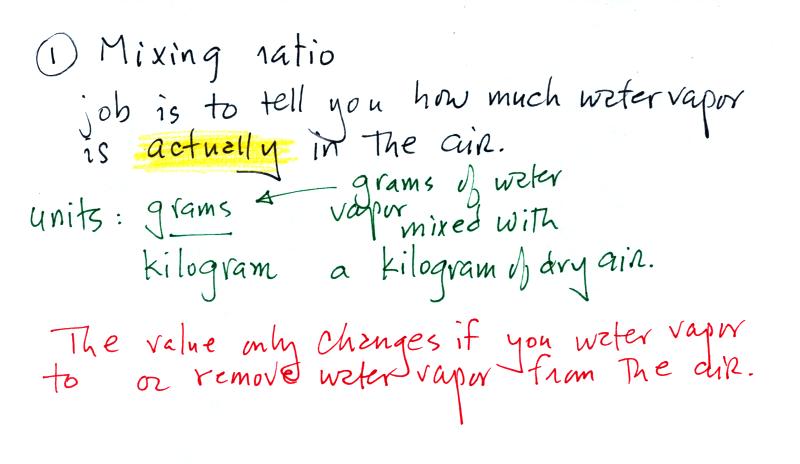
Mixing ratio ( r )
The bottom half of the figure below can
be found on p. 83 in the ClassNotes.
Mixing ratio tells you how much water vapor
is actually
in the air. Mixing ratio has units of grams of
water vapor per kilogram of dry air (the amount of water vapor
in grams mixed with a kilogram of dry air). A kilogram
of air is about one cubic meter of air (about one cubic yard
of air). Mixing ratio is
basically the same idea as teaspoons of sugar mixed in a
cup of tea. We'll use a lower case
r to represent mixing ratio.

The value of the mixing ratio won't change
unless you add water vapor to or remove water vapor from the
air. Warming the air won't change the mixing
ratio. Cooling the air won't change the mixing ratio (with one exception
- when the air is cooled below its dew point temperature and
water vapor starts to condense). Since the mixing
ratio's job is to tell you how much water vapor is in the air,
you don't want it to change unless water vapor is actually
added to or removed from the air.
Saturation mixing ratio ( rS )
Saturation mixing ratio is just an upper limit
to how much water vapor can be found in air, the air's
capacity
for water vapor. It's a property of air and depends on
the air's temperature; warm air can potentially hold
more water vapor than cold air. It doesn't
say anything about how much water vapor is actually in the air
(that's the mixing ratio's job). This
variable has the same units: grams of water vapor per kilogram
of dry air. Saturation mixing ratio values for different
air temperatures are listed and graphed on p. 86 in the
ClassNotes.
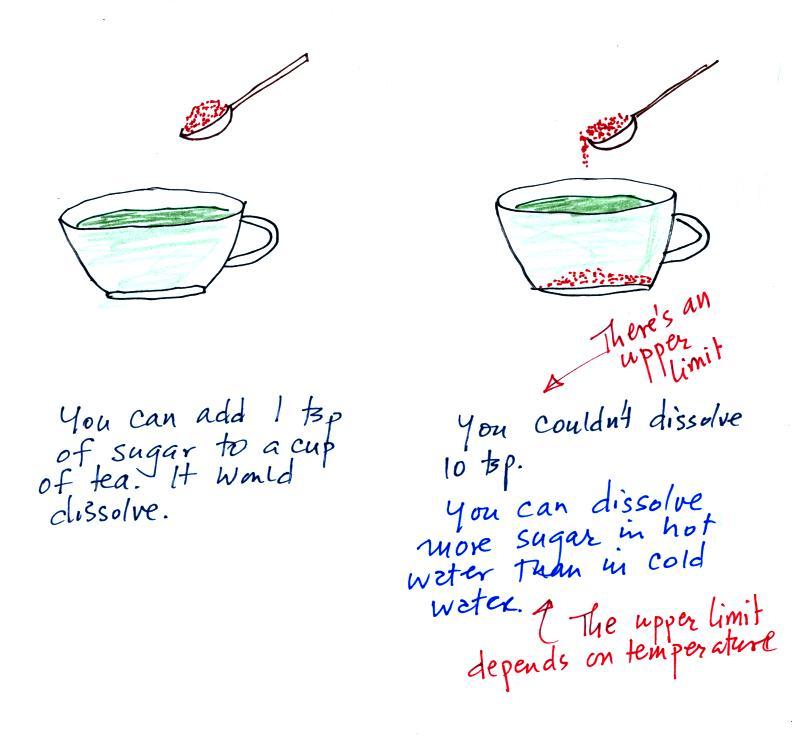
The sugar dissolved in tea analogy is still
helpful. Just as is the case with water vapor in air,
there's a limit to how much sugar can be dissolved in a cup of
hot water. And not only that, the amount depends on
temperature: you can dissolve more sugar in hot water than in cold
water.
The dependence of saturation mixing ratio on air
temperature is illustrated below:
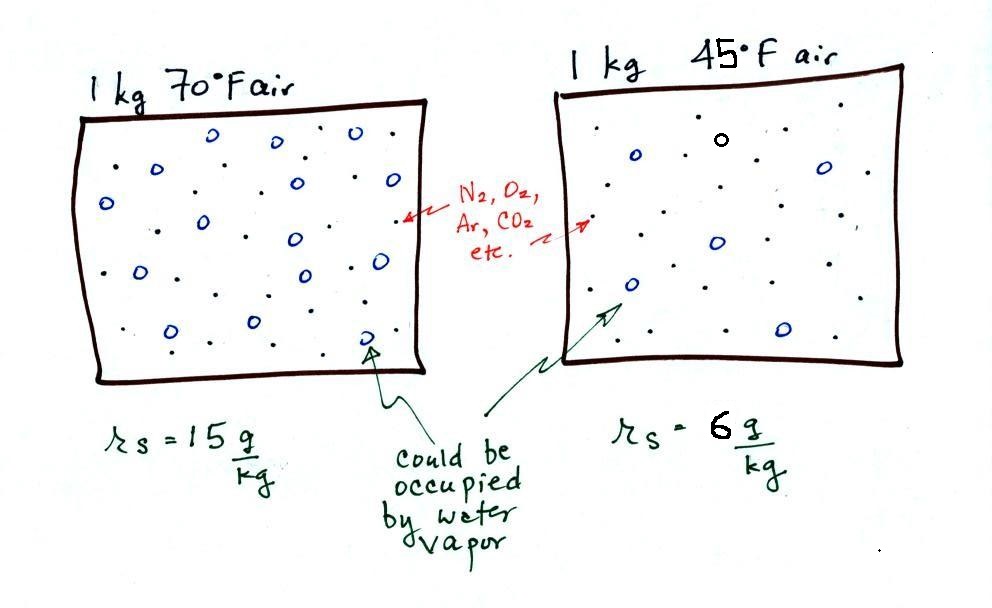
The small specks represent all
of the gases in air except for the water vapor. Each of
the open circles represents 1 gram of water vapor
that the air could potentially hold. There are 15 open
circles drawn in the 1 kg of 70 F air; each 1 kg of 70 F air
could hold up to 15 grams of water vapor. The 45 F air
only has 6 open circles; this cooler air can only
hold up to 5 grams of water vapor per kilogram of dry air.
The numbers 15 and 5 came from the table on p. 86.
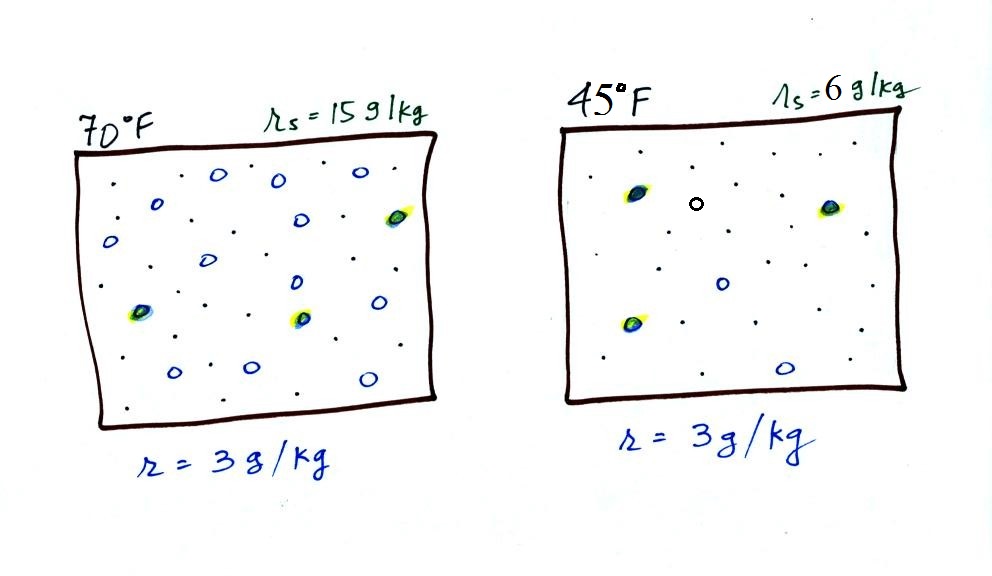
Now we have gone and actually
put some water vapor into the volumes of 70 F and 40 F air (the
open circles are colored in). The same amount, 3 grams of
water vapor, has been added to each volume of air. Three
of the open circles have been colored in. The mixing
ratio, r, is 3 g/kg in both cases. One of the
figures is almost filled to capacity, with water vapor the other
is not. That's basically what the 3rd humidity variable,
relative humidity, tells us
Relative humidity (RH)
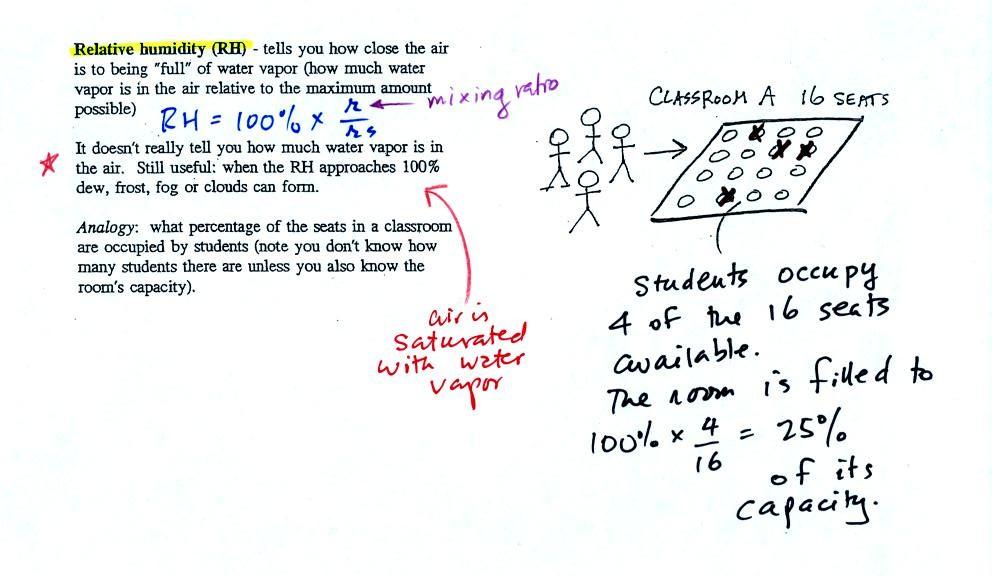 |
The relative humidity is the
variable most people are familiar with. It tells you how
"full" the air is with water vapor, how close it is to
being filled to capacity with water vapor, how
close the air is to being "saturated" with water
vapor. RH has units of %.
In the analogy (sketched on the right hand side of p. 83 in
the photocopied notes) 4 students wander into Classroom A which
has 16 empty seats. Classroom A is filled to
25% of its capacity. You can think of 4, the
actual number of students, as being analogous to the mixing
ratio. The classroom capacity is analogous to the
saturation mixing ratio. How full the room is is analogous
to the relative humidity.
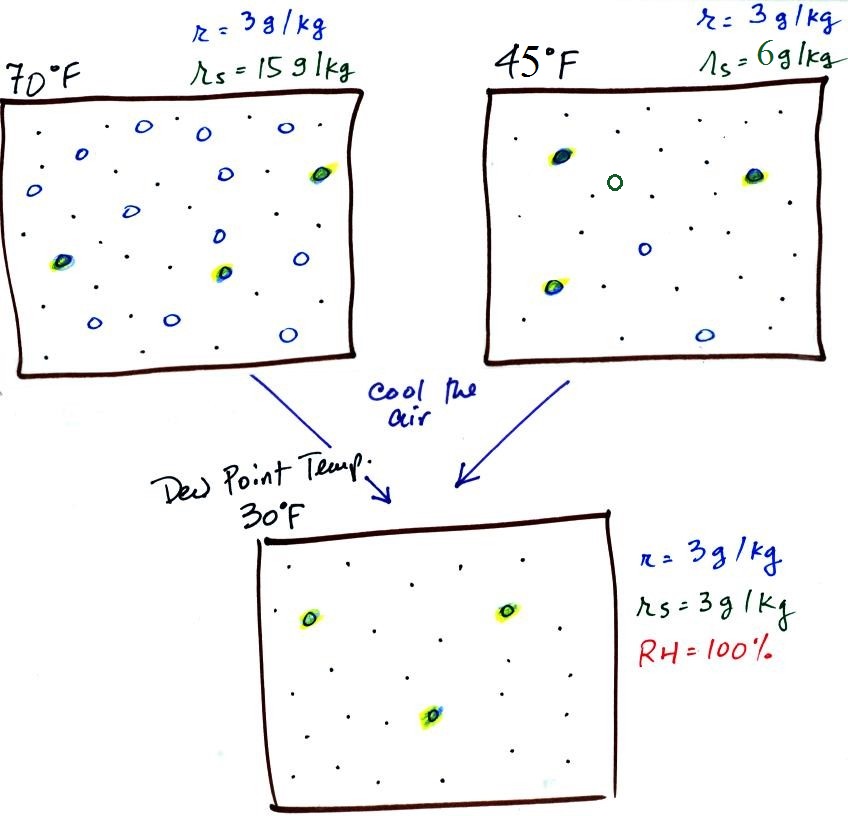
The figure below goes back to the volumes (1 kg each) of 70 F
and 40 F air that could potentially hold 15 grams or 5 grams of
water vapor.
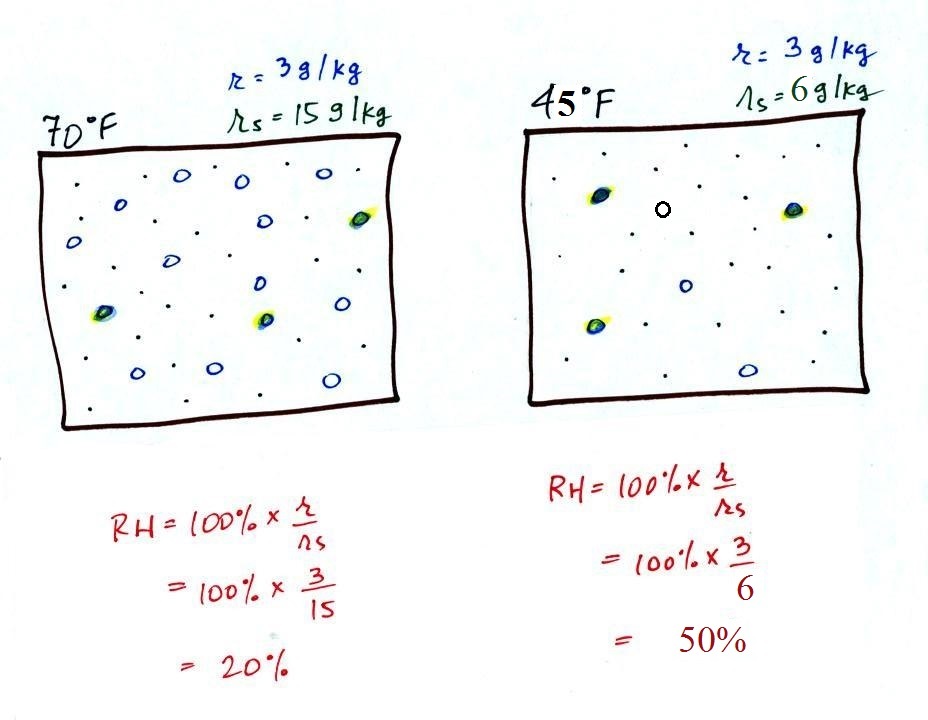
Both the 70 F and the 40 F air each contain 3 grams of water
vapor. The 70 F air is only filled to 20% of capacity (3 of
the 15 open circles is colored in) because this warm air's
capacity, the saturation mixing ratio, is large. The RH in
the 40 F is 60% even though it has the same actual amount of water
vapor because the 40 F air can't hold as much water
vapor and is closer to being saturated.
Something important to note: RH
doesn't really tell you how much water vapor is actually in
the air. The two volumes
of air above contain the same amount of water vapor (3 grams per
kilogram) but have very different values of relative
humidity. You could just as easily have two volumes of air
with the same relative humidity but different actual amounts of
water vapor.
What is the RH good for if it doesn't tell you how much
moisture is in the air? When the RH reaches 100% dew, fog,
and clouds form. RH tells you whether clouds or fog are
about to form or not.
Dew point temperature
The dew point temperature has
two jobs. First it gives you an idea of the actual amount
of water vapor in the air. In this respect it is
just like the mixing ratio. If the dew point temperature
is low the air doesn't contain much water vapor. If it is
high the air contains more water vapor. This is something
we learned early in the semester.
The dew point is a temperature and has units of
oF or oC
Second the dew point tells you how much you
must cool the air in order to raise the RH to 100% (at which
point a cloud, or dew or frost, or fog would form). This
idea of cooling the air until the RH increases to 100% is
important and is something we will use a lot.
If we cool the 70 F air or the 40 F air to 30
F we would find that the saturation mixing ratio would decrease
to 3 grams/kilogram. Since the air actually contains 3
g/kg, the RH of the 30 F air would become 100%. The 30 F
air would be saturated, it would be filled to capacity with
water vapor. 30 F is the dew point temperature for 70 F
air that contains 3 grams of water vapor per kilogram of dry
air. It is also the dew point temperature for 40 F air
that contains 3 grams of water vapor per kilogram of dry air.
Because both volumes of air had the same amount of water
vapor, they both also have
the same dew point temperature.
Now back to the
student/classroom analogy.
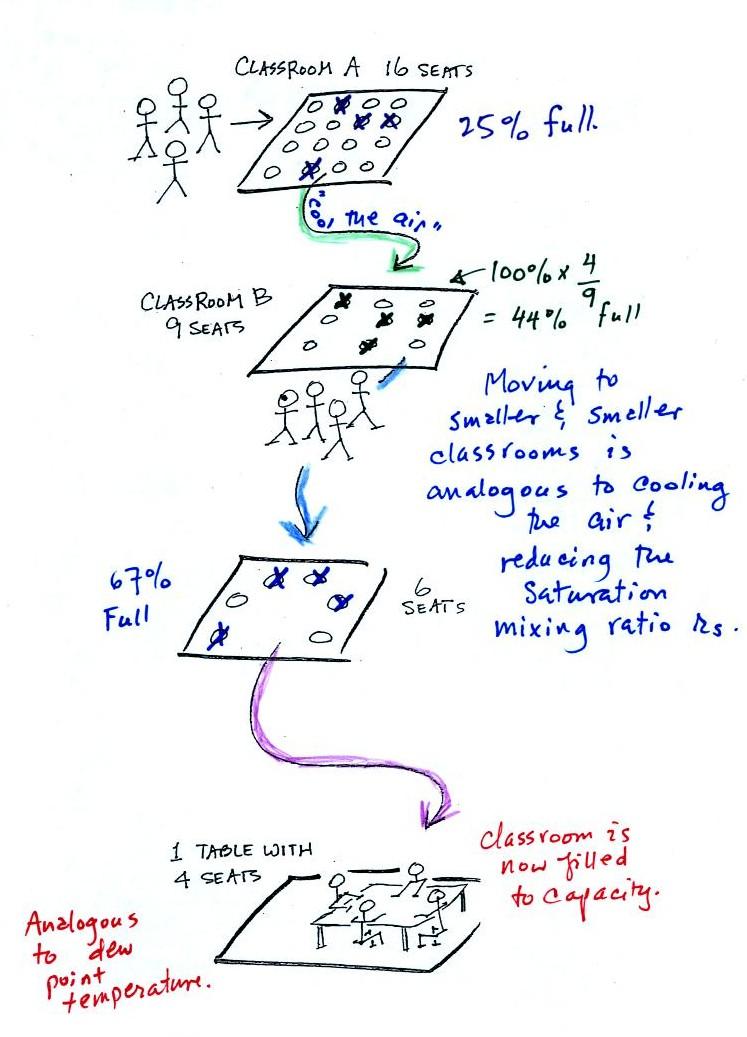
The 4 students move into classrooms of
smaller and smaller capacity. The decreasing capacity of
the classrooms is analogous to the decrease in
saturation mixing ratio that occurs when you cool air.
Eventually the students move into a classroom that they just
fill to capacity. This is analogous to
cooling the air to the dew point. Seems like
kind of a dumb analogy, though, after a few example problems,
we'll see that it is not.
I'm hoping we'll have enough time to work a couple of
humidity example problems. This is the way to
become more familiar with the humidity variables and how
they behave and what causes them to change value.
We'll make use of the table of saturation mixing
ratios on p. 84 and the charts on pps 85 & 86 in the
ClassNotes.
Humidity example problem #1
There are 4 humidity variables (mixing
ratio, saturation mixing ratio, relative humidity,
and dew point temperature). Generally I'll
give you values for two of them and you'll need to
figure out values for the other two.
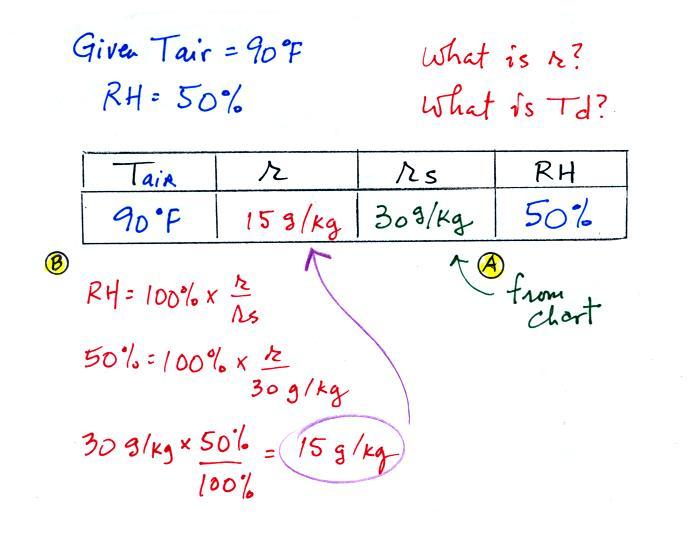
Here are the starting conditions for this first
problem
Tair = 90 F
|
r = 6 g/kg
|
RH = ?
|
Td = ?
|
We start by entering the data we were given
Anytime you know the air's temperature
you can look up the saturation mixing ratio value on a chart
(such as the one on p. 86 in the ClassNotes); the saturation
mixing ratio is 30 g/kg for 90 F air. 90 F air could
potentially hold 30 grams of water vapor per kilogram of dry
air (it actually contains 6 grams per kilogram in this
example).
Once you know mixing ratio and saturation mixing ratio
you can calculate the relative humidity (you divide the
mixing ratio by the saturation mixing ratio, 6/30, and
multiply the result by 100%). You ought to be able to
work out the ratio 6/30 in your head (6/30 = 1/5 =
0.2). The RH is 20%.
The numbers we just figured out are shown on the top line
below.
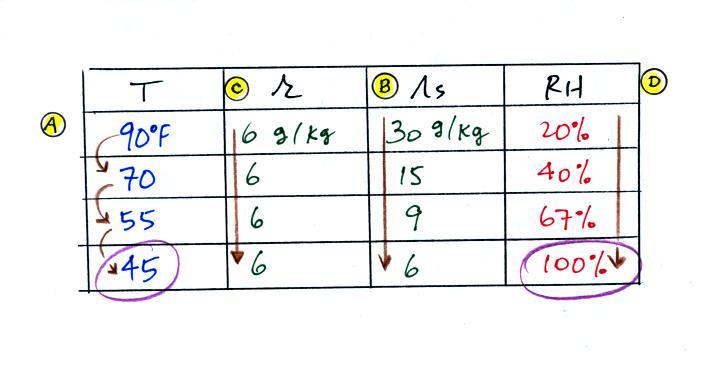
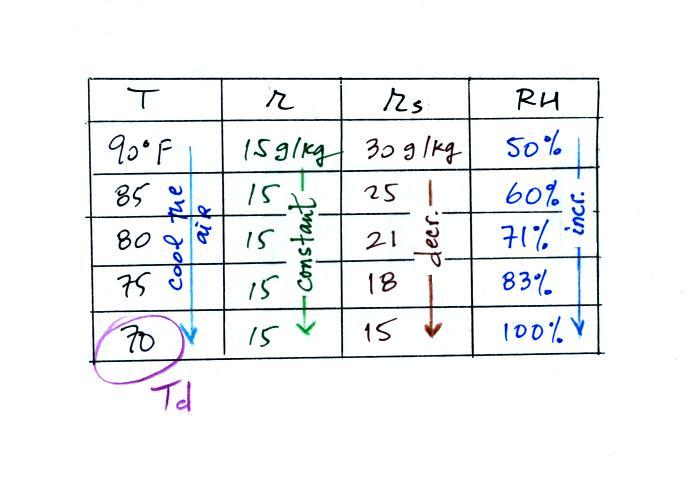
(A) To figure out the dew point, we imagine
cooling the air from 90F to 70F, then to 55F, and finally
to 45F. Note the effect this has on the mixing
ratio, the saturation mixing ratio and the relative
humidity.
(B) At each step we looked up the saturation mixing
ratio and entered it on the chart. Note that the
saturation mixing ratio values decrease as the
air is cooling.
(C) The mixing
ratio (r) doesn't change as we cool the air.
The only thing that changes r is adding or removing water
vapor and we aren't doing either. This is probably the
most difficult concept to grasp.
(D) Note how the relative humidity is increasing as we
cool the air. The air still contains the same amount
of water vapor it is just that the air's capacity is
decreasing.
Finally at 45 F the RH becomes 100%. This is the
dew point. The dew point temperature is 45 F
What would happen if we cooled the air below the
dew point temperature?
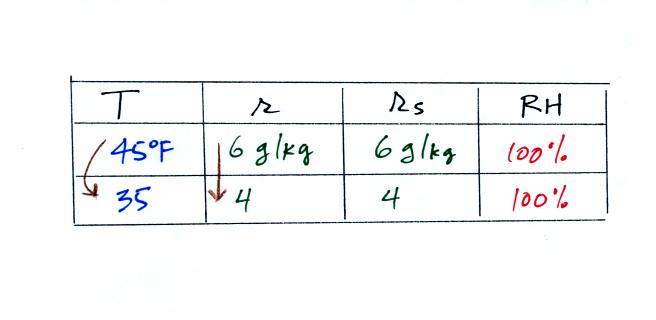
35 F air can't hold the 6 grams of water
vapor that 45 F air can. You can only "fit" 4 grams of
water vapor into the 35 F air. The remaining 2 grams
would condense. If this happened at ground level the
ground would get wet with dew. If it happens above the
ground, the water vapor condenses onto small particles in
the air and forms fog or a cloud. Because water vapor
is being taken out of the air (the water vapor is turning
into water), the mixing ratio will decrease from 6 g/kg to 4
g/kg. As you cool air below the dew point, the RH
stays constant at 100% and the mixing ratio decreases.
In many ways cooling moist air is liking squeezing
a moist sponge
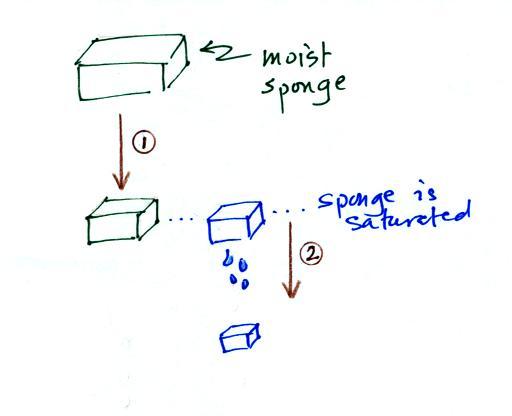
Squeezing the sponge and reducing its
volume is like cooling moist air and reducing the saturation
mixing ratio. At first (Path 1 in the figure) when you
squeeze the sponge nothing happens, no water drips
out. Eventually you get to a point where the sponge is
saturated. This is like reaching the dew point.
If you squeeze the sponge any further (Path 2) water will
begin to drip out of the sponge (water vapor will condense
from the air).
Humidity example problem #2
Tair = 90 F
|
r =
?
|
| RH = 50% |
Td =
?
|
The problem is worked out in detail below
First you fill in the air temperature and the RH data
that you are given.
(A) since you know the air's temperature you can look up the
saturation mixing ratio (30 g/kg).
(B) Then you might be able to figure out the mixing
ratio in your head. Air that could hold up to 30 g/kg
of water vapor is filled to 50% of its capacity. Half
of 30 is 15, that is the mixing ratio. Or you can
substitute into the relative humidity formula and solve for
the mixing ratio. The details of that calculation are
shown above at B.
Finally you imagine cooling the air (I added more intermediate temperatures
in the table above than we use in class).
Notice how the saturation mixing ratio decreases, the mixing
ratio stays constant, and the relative humidity increases as
the air is cooled. In this example the RH
reached 100% when the air had cooled to 70 F. That is
the dew point temperature.
What
does the difference Tair - Td tell you about the
relative humidity?
We
can use results from humidity problems #1
and #2 to learn and understand a useful
rule.
In the first example the difference between the air and
dew point temperatures was large (45 F) and the RH was low
(20%).
In the 2nd problem the difference between the air and dew
point temperatures was smaller (20 F) and the RH was higher
(50%).
The easiest way to remember this rule might be to remember
the case where there is no difference between the air and
dew point temperatures.
The RH then would be 100%.
This is a good place to stop. I'll include one
additional example below just in case you want to give it
a try on your own.
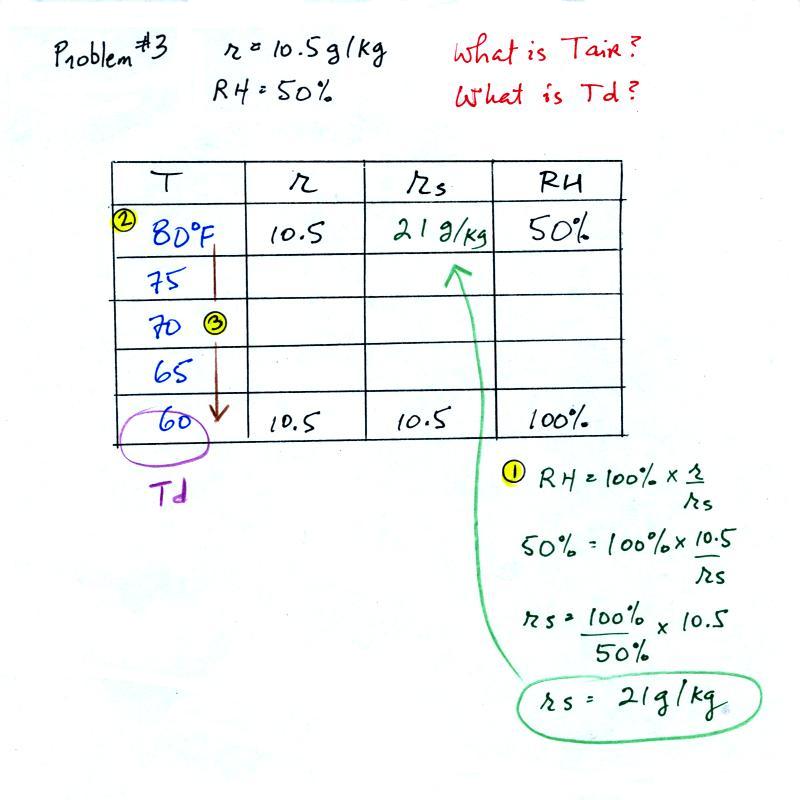
Humidity example problem #3
Tair
= ?
|
r = 10.5 g/kg
|
| RH = 50% |
Td =
?
|
You're given the the mixing ratio = 10.5 g/kg and a
relative humidity of 50%. You
need to figure out the air temperature and the dew point
temperature. Give it a try. A step by
step solution is given below:
(1) The air contains 10.5 g/kg of water vapor. This is
50% (half) of what the air could potentially hold. So
the air's capacity, the saturation mixing ratio must be 21
g/kg (you can either do this in your head or use the RH
equation following the steps shown above).
(2) Once you know the saturation mixing ratio you can look
up the air temperature in a table (80 F air has a saturation
mixing ratio of 21 g/kg)
(3) Then you imagine cooling the air until the RH becomes
100%. This occurs at 60 F. The dew point is 60 F