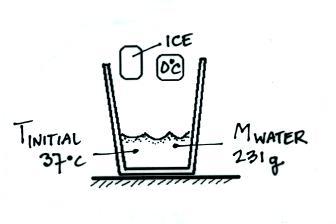
In the figure below the ice has
been added to the warm water and melted. We are at the "midway"
point of the experiment; the ice has turned from a solid to a liquid
but its temperature hasn't changed, it is still 0oC.
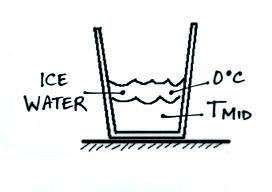

The energy needed to melt the ice
is:


This energy came from the warm
water and cause the water to cool (from Tinitial to Tmid). We
could use the following equation to determine how much energy was taken
from the water (we won't do the calculation because we don't know what
Tmid is).


Heat will continue to flow from the
warm water into the 0o
C ice water. Energy will flow until all of the water
has the same temperature, Tfinal.
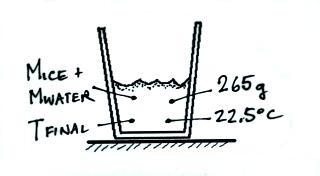
So the warm water will lose an additional amount of energy:



The energy is used to warm the
melted ice to Tfinal:
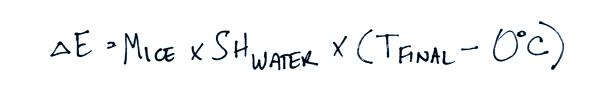
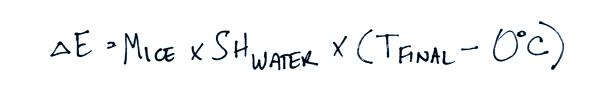
Now we will combine all the
separate terms. Energy was removed from the water to first melt
the ice and then to warm the ice water to Tfinal. The toal energy
lost by the warm water is:
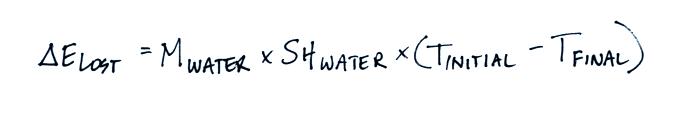
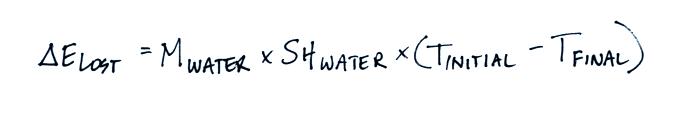
We perform the experiment in an
insulated cup and we assume that all of the energy lost by the warm
water was used to melt ice and warm up the ice water; no energy flowed
from the cup into the cooler air in the room. We'll add the 1st
and 4th equations above together:
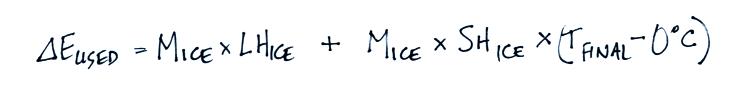
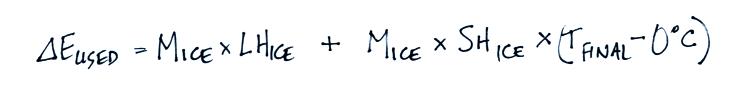
We'll set the energy lost and
energy used equations equal to each other. This gives us an
energy balance equation that can used to determine LHice:
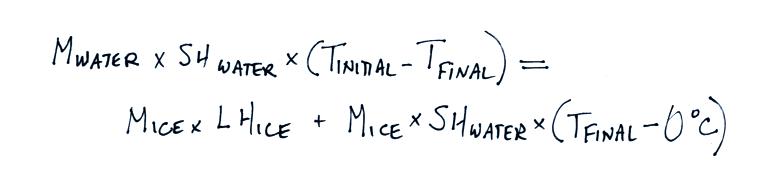

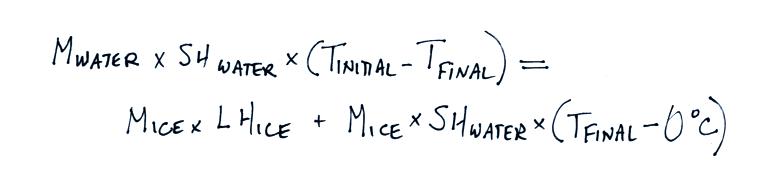
The specific heat of water is 1
cal/gm oC. You can plug this value
together with your measured values for Mwater, Mice, Tinitial and
Tfinal
and solve for LHice. An example calculation using the data shown
in the figures above is given below. The known value for the
latent heat of fusion of ice is 80 calories/gram so the measured value
below compares pretty well.
