Friday Sept. 28, 2012
click here to download  today's notes in a more  printer friendly format

Just about the best version of Stand By Me you'll ever hear (in my opinion at least) from Playing for Change.


When you add energy to an object, the object will usually warm up (or if you take energy from an object the object will cool).  It is relatively easy to come up with an equation that allows you to figure out what the temperature change will be (this is another equation I'll write on the board before  the next quiz if you ask me to - try to understand it, you don't have to memorize it).




The temperature change, ΔT,  will first depend on how much energy was added, ΔE.  This is a direct proportionality, so ΔE is in the numerator of the equation (ΔE and ΔT are both positive when energy is added, negative when energy is removed)

When you add equal amounts of energy to large and small  pans of water, the small pan will heat up more quickly.  The temperature change, ΔT, will depend on the amount of water, the mass.  A small mass will mean a large ΔT, so mass should go in the denominator of the equation. 

Specific heat is what we use to account for the fact that different materials react differently when energy is added to them.  A material with a large specific heat will warm more slowly than a material with a small specific heat.  Specific heat has the same kind of effect on ΔT as mass.  Specific heat is sometimes called "thermal mass" or "thermal capacity."  You can think of specific heat as being thermal inertia - a substance with high specific heat, lots of thermal inertia, will be reluctant to change temperature.

Here's an important example that will show the effect of specific heat (middle of p. 45).


Equal amounts of energy (1000 calories, note that calories are units of energy) are added to equal masses (500 grams) of water and soil.  We use water and soil in the example because most of the earth's surface is either ocean or land. Before we do the calculation, try to guess which material will warm up the most.  Everything is the same except for the specific heats.  Will water with its 5 times larger specific heat warm up more or less than the soil?

Here are the details of the calculation.

With its higher specific heat, the water doesn't heat up nearly as much as the soil.  If we had been removing energy the wouldn't cool off as much as the soil would.

These different rates of warming of water and soil have important effects on regional climate.


Oceans moderate the climate.  Cities near a large body of water won't warm as much in the summer and won't cool as much during the winter compared to a city that is surrounded by land.  Water's ΔT is smaller than land's because water has higher specific heat.
The yearly high and low monthly average temperatures are shown at two locations above.  The city on the coast has a 30o F annual range of temperature (range is the difference between the summer and winter temperatures).  The city further inland (assumed to be at the same latitude and altitude) has an annual range of 60o F.  Note that both cities have the same 60o F annual average temperature.  We'll see a much more dramatic example of the moderating effect of water on climate in a couple of weeks.

Here's another situation where you can take advantage of water's high specific heat to moderate "micro climate."



I usually plant tomatoes in my vegetable garden in February so that they can start to make tomatoes before it starts to get too hot in May.  In February it can still get cold enough to kill tomatoes (the brocolli and lettuce in the background can handle a light frost) so you have to protect them.





Here's one way of doing that.  You can surround each plant with a "wall o water"  -  a teepee like arrangement that surrounds each plant.  The cylinders are filled with water and they take advantage of the high specific heat of water and won't cool as much as the air or soil would during a cold night.  The walls of water produce a warm moist microclimate that the tomato seedlings love.  The plastic is transparent so plenty of sunlight can get through.

Adding energy to an object will usually cause it to warm.  But there is another possibility (bottom p. 45),  the object could change phase (change from solid to liquid or gas).  Adding energy to ice might cause the ice to melt.  Adding energy to water could cause it to evaporate.
The equation at the bottom of the figure above allows you to calculate how much energy is required to melt ice or evaporate water or sublimate dry ice.  You multiply the mass by the latent heat, a variable that depends on the particular material that is changing phase.  The latent heat of vaporization (evaporation) is the energy required to evaporate 1 gram of a material.

If you add energy to or remove energy from an object, the object will usually change temperature.  You can calculate the temperature change if you know the object's mass and its specific heat.  That's the equation we used in the example calculation above.  It's shown again below.



We conducted an experiment in the last part of the class and we needed to be able to measure ΔE.  We'll stick a thermometer into the object and measure any changes in temperature that occur.

If you know the mass and specific heat of an object and measure a change in temperature you can use the rearranged equation in the figure above to calculate how much energy was added to or removed from the object.

And on to the in-class experiment.  A couple of groups of students from the class were nice enough to volunteer to perform the experiment.  They'll  be able to write a report about the experiment and use the data you collected to satisfy the Experiment Report part of the Writing Requirements.  I.e. they won't have to worry about checking out materials and doing Expt. #1, #2, or #3.  A couple of the students had done Expt. #1.  I got to thinking after class that they deserved something for their effort and I think I'll give them each a Green Card.

Here's the object of the experiment:


The students that are doing Experiment #2 are doing something similar, they are measuring the latent heat of fusion of ice, the energy needed to melt one gram of ice. 

Here's the data that one of the groups collected in class.  This will be hard to figure out even after having cleaned things up a bit after class.


So here's a step by step explanation of what the students did:
(a)


Some room temperature water poured into a styrofoam cup weighed 177.1 g.  The cup itself weighed 4.1 g, so they had 173.0 g of water.  The water's temperature was measured with the thermometer and was 24.5 C (room temperature).

(b)
Some liquid nitrogen was poured into a second smaller styrofoam cup.  That weighed 37.0 g.  Subtracting the 2.0 g weight of the cup means we had 35.0 g of liquid nitrogen. 

We don't need to measure the temperature of the liquid nitrogen (doing so would probably destroy the thermometer).  It had already warmed up as much as it ccould ( to -320 F or something like that).  Any additional energy added to the liquid nitrogen will cause it to evaporate.

(c)
After the liquid nitrogen had evaporated the water's temperature was remeasured.  It had dropped to 14.0 C. 

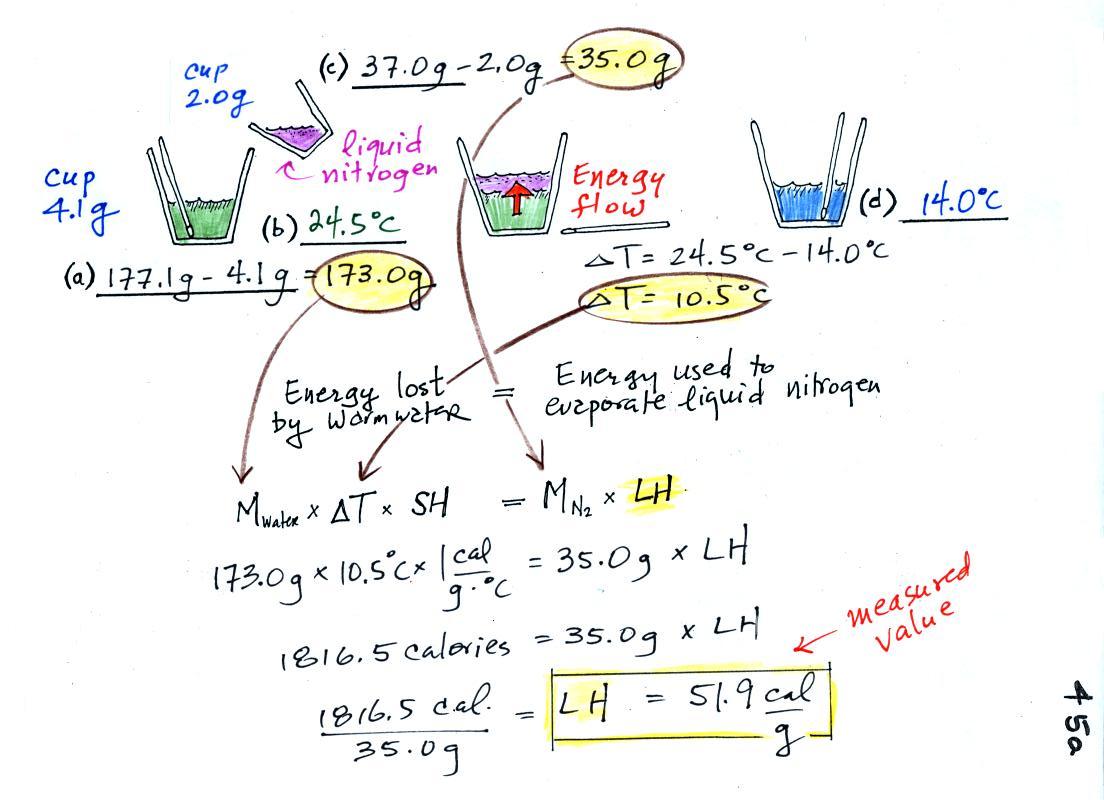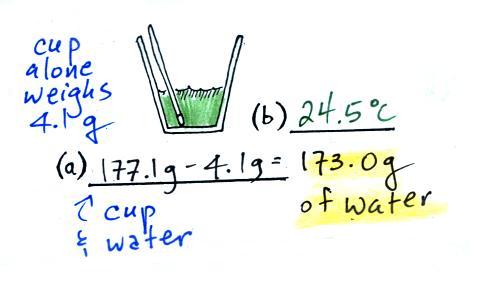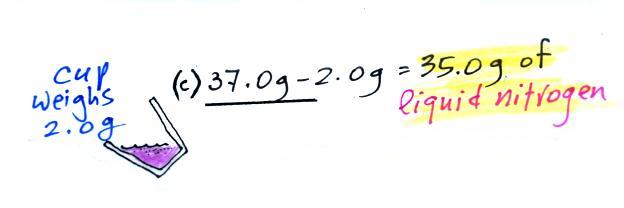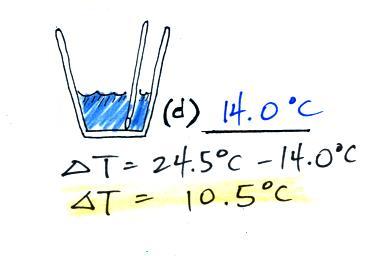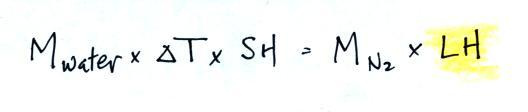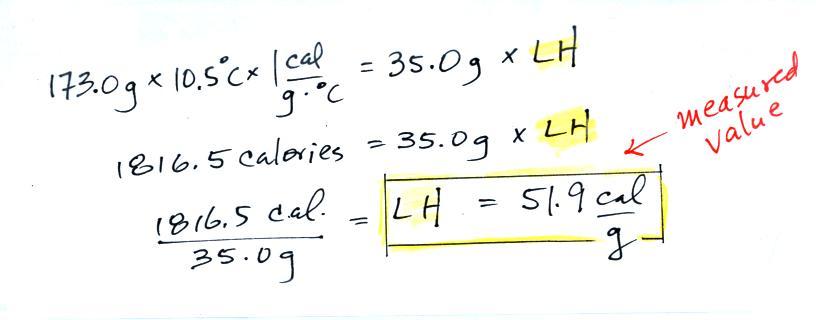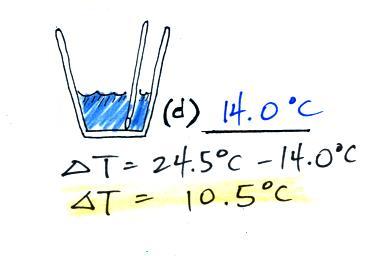
We started out with water that was 24.5 C, so that is a temperature drop of 10.5 C.

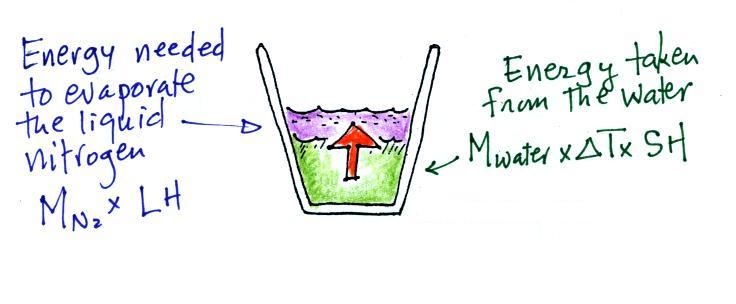
It takes energy to turn liquid nitrogen into nitrogen gas.  The energy needed will be taken from the water (the red arrow below, energy naturally flows from hot to cold). 


Because the experiment was performed in an insulated sytrofoam cup we will assume all of the energy taken from the water is used to evaporate nitrogen.  Minimal energy flows into the room air or anything like that.  We will set the two equations above equal to each other.  This is an energy balance equation.

We know the mass of the nitrogen that we started with and that was eventually evaporated (41.9 g) and the mass of the water (184.0 g).  We measured the ΔT (12.0 C) and we know the specific heat of water (1 cal/g C).  We substitute them into the equation above and solve for LH, the latent heat of vaporization of liquid nitrogen.  Here are the details of the calculation:
A responsible & trustworthy student in the class (though not a Buddhist monk it turns out) informed us that the known value is 48 cal/g, so this measured value is pretty close to the known value.
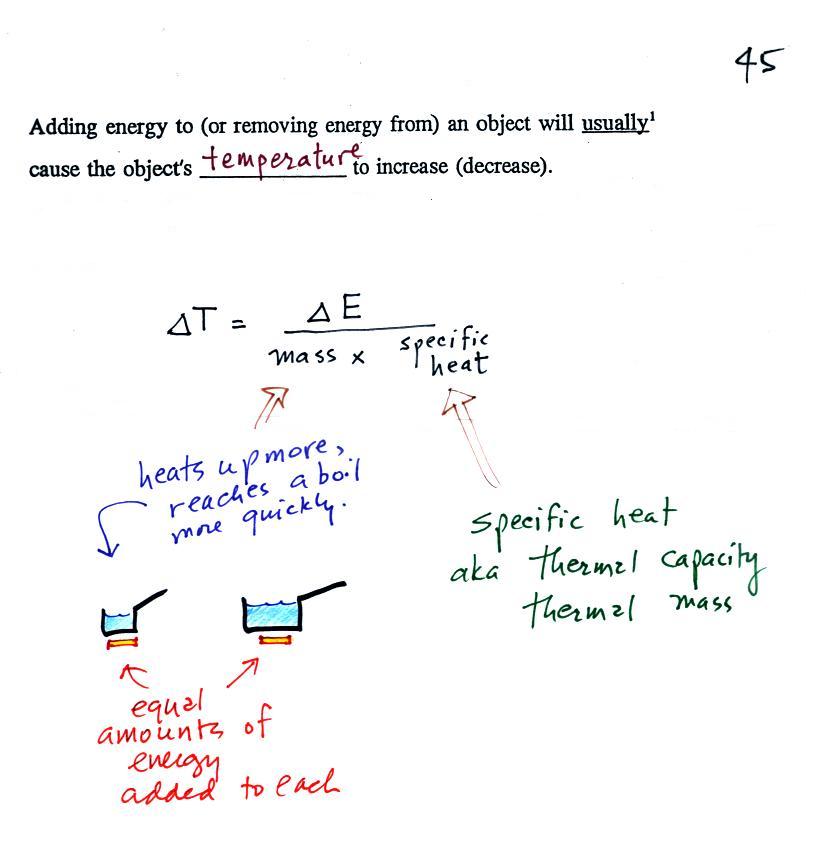
You add energy to something and its temperature increases.  The figure below (p. 46 in the ClassNotes) shows you what happens inside an object when it's temperature changes (a picture from a previous semester).


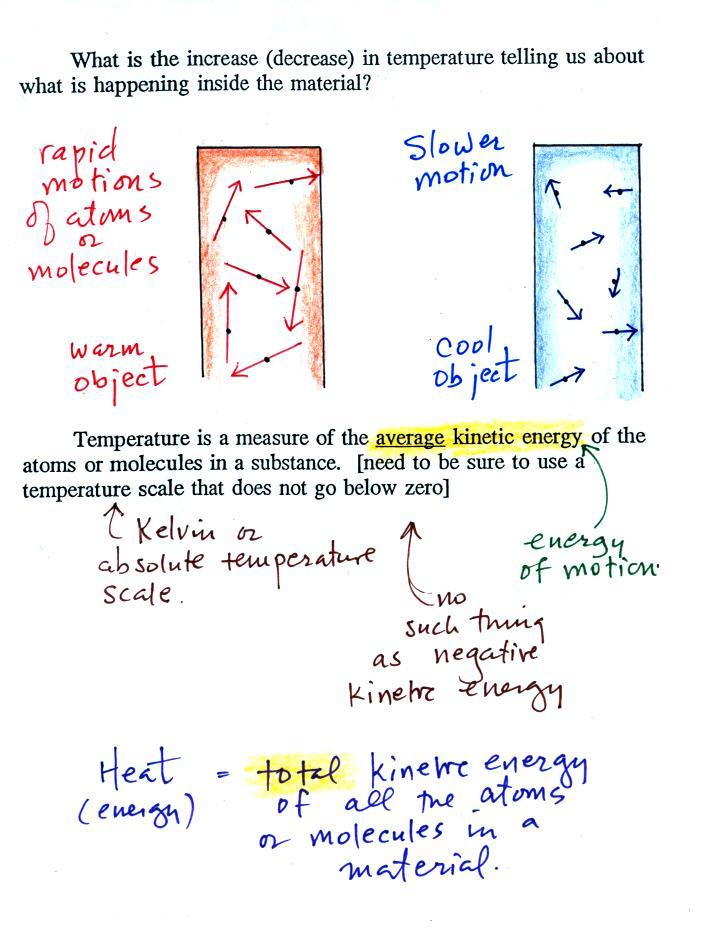
The atoms or molecules inside the warmer object will be moving more rapidly (they'll be moving freely in a gas, just "jiggling" around in a solid).  Temperature provides a measure of the average kinetic energy of the atoms or molecules in a material. 

You need to be careful what temperature scale you use when using temperature as a measure of average kinetic energy.  You must use the Kelvin temperature scale because it does not go below zero (0 K is known as absolute zero). The smallest kinetic energy you can have is zero kinetic energy.  There is no such thing as negative kinetic energy.

You can think of heat as being the total kinetic energy of all the molecules or atoms in a material.

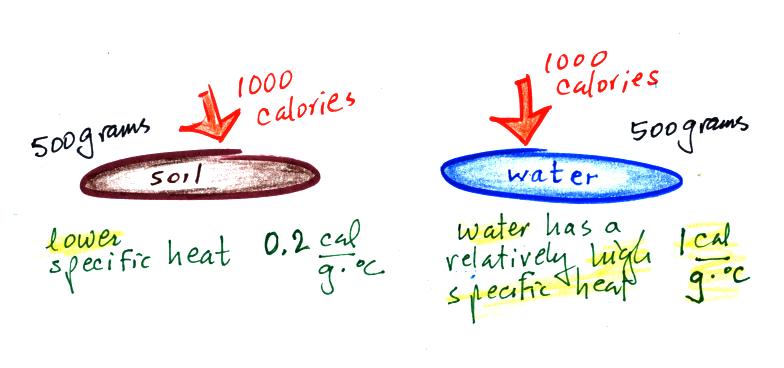
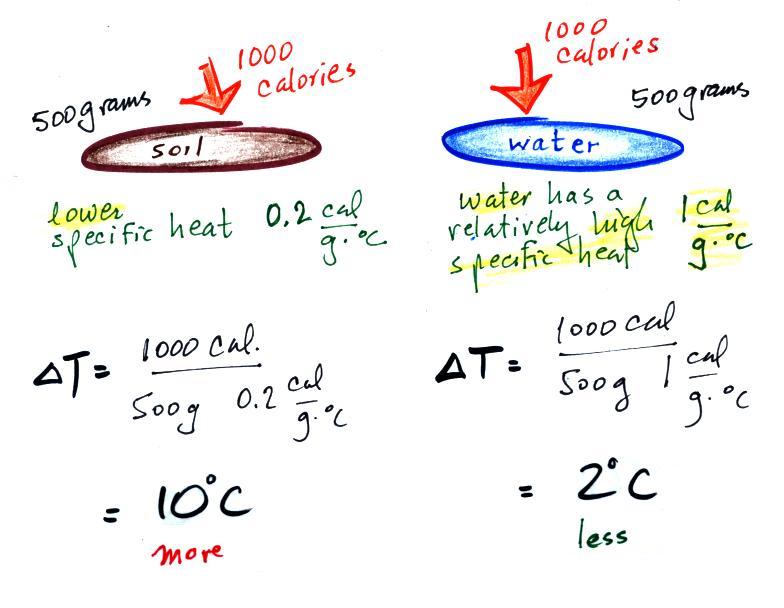
This next figure might make clearer the difference between temperature (average kinetic energy) and heat (total kinetic energy).




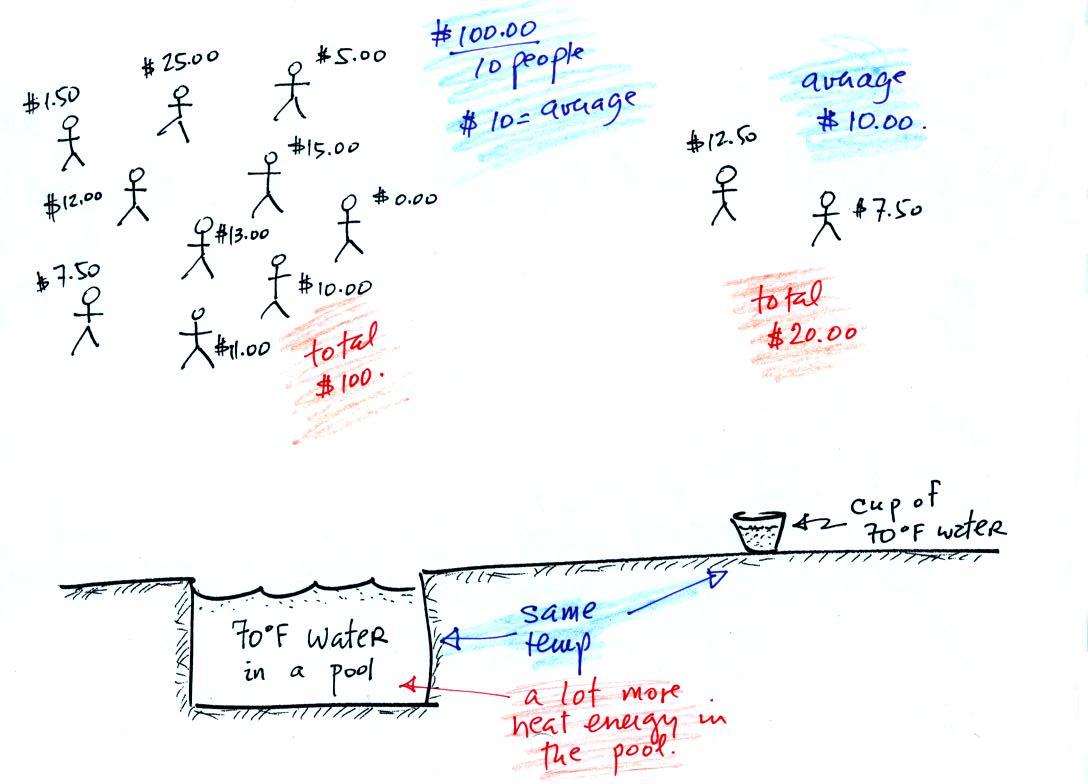
A cup of water and a pool of water both have the same temperature.  The average kinetic energy of the water molecules in the pool and in the cup are the same.  There are a lot more molecules in the pool than in the cup.  So if you add together all the kinetic energies of all the molecules in the pool you are going to get a much bigger number than if you sum the kinetic energies of the molecules in the cup.  There is a lot more stored energy in the pool than in the cup.  It would be a lot harder to cool (or warm) all the water in the pool than it would be the cup.

In the same way the two groups of people and money (the people represent atoms or molecules and the money is analogous to kinetic energy).  Both groups have the same same average amount of money per person (that's analogous to temperature).  The $100 held by the larger group at the left is greater than the $20 total possessed by the smaller group of people on the right (total amount of money is analogous to heat). 


And finally, speaking of temperature scales

You should remember the temperatures of the boiling point and freezing point of water on at least the Fahrenheit and  Celsius scales (and the Kelvin scale if you want to).  300 K is a good easy-to-remember value for the global annual average surface temperature of the earth.  That's a number you should try to remember also (and remember that temperatures never go below 0 K).


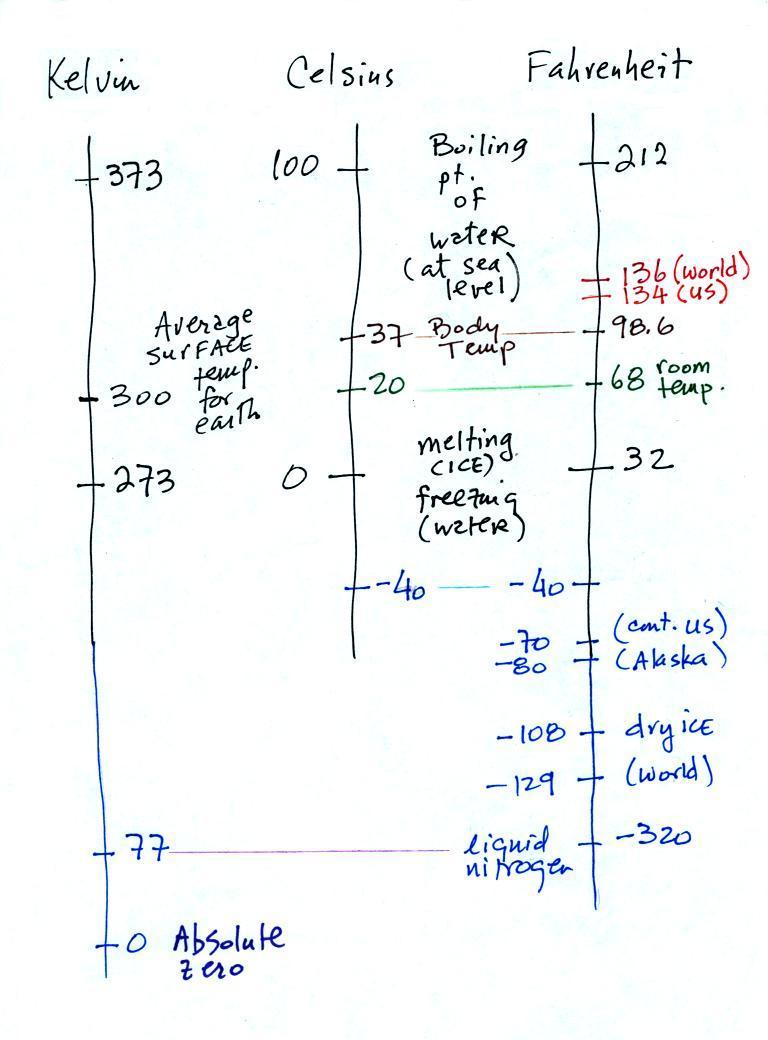
You certainly don't need to try to remember all these numbers.  The world high temperature record was set in Libya, the US record in Death Valley (low altitude [below sea level], surrounded by land, and near 30 degrees latitude).  I'll do some checking but I think that someone might have decided that the 136 F world record value wasn't reliable and the US value 134 F might be the new world record. 

The continental US cold temperature record of -70 F was set in Montana and the -80 F value in Alaska.  The world record -129 F was measured at Vostok station in Antarctica.  This unusually cold reading was the result of three factors: high latitude, high altitude, and location in the middle of land rather than being near or surrounded by ocean (remember water moderates climate).   Liquid nitrogen is cold but it is still quite a bit warmer than absolute zero.  Liquid helium gets within a few degrees of absolute zero, but it's expensive and there's only a limited amount of helium available.  So I would feel guilty bringing some to class.