Wed.,  Sep. 12, 2012
click here to download today's notes in a more printer friendly format

Some mariachi music to celebrate Mexican Independence Day (from Spain) coming up this weekend (Sept. 16).  You heard
Cancion del Mariachi, and  El Picador (World Drifts In) (2:47).  Not nearly enough time for El Cascabel (7:05) or  Crystal Frontier (9:13) but you can listen to them on your own if you want to.  All of these videos featuring Calexico and Mariachi Luz de Luna were recorded at the  Barbican Theater in London in 2002.

Quiz #1 is Wednesday next week (Sept. 19) and the Quiz #1 Study Guide is now online.  Quiz #1 will also cover material on the Practice Quiz Study Guide.  Note that there is now an additional review scheduled for next week: Tuesday afternoon (Sept. 18) from 2 - 2:50 pm in Saguaro Hall 225.

Quite a lot of material to cover today.  Our objective will be to understand why warm air rises and cold air sinks. 



Hot air balloons rise (they also sink), so does the relatively warm air in a thunderstorm updraft (it's warmer than the air around it).   Conversely cold air sinks.  The surface winds caused by a thunderstorm downdraft (as shown above) can reach speeds of 100 MPH (stronger than most tornadoes) and are a serious weather hazard.

A full understanding of these rising and sinking motions is a 3-step process (the following is from the bottom part of p. 49 in the photocopied ClassNotes). 



We will first learn about the ideal gas law.  That is an equation that tells you which properties of the air inside a balloon work to determine the air's pressure.  Then we will look at Charles' Law, a special situation involving the ideal gas law (air temperature volume, and density change together in a way that keeps the pressure inside a balloon constant).  Then we'll learn about the vertical forces that act on air (an upward and a downward force).

Students working on Experiment #1 will need to understand the ideal gas law to be able to fully explain why/how their experiment works.

The figure above makes an important point: the air molecules in a balloon "filled with air" really take up very little space.  A balloon filled with air is mostly empty space.  It is the collisions of air molecules traveling at 100s of miles per hour with the inside walls of the balloon that keep it inflated.



Up to this point in the semester we have been thinking of pressure as being determined by the weight of the air overhead.  Air pressure pushes down against the ground at sea level with 14.7 pounds of force per square inch.  That's a perfectly good concept.

We then went a bit further and tried to imagine the weight of the atmosphere pushing down on a balloon sitting on the ground.  If you actually do push on a balloon you realize that the air in the balloon pushes back with the same force.  Air everywhere in the atmosphere pushes upwards, downwards, and sideways. 



Step #1 - The ideal gas law
The ideal gas law equation is another way of thinking about air pressure, sort of a microscopic scale version.  We ignore the atmosphere and concentrate on just the air inside the balloon.  We'll end up with an equation.  Pressure (P) will be on the left hand side of the equation. The right hand side of the equation will show how various properties of the air work to determine the air pressure.



In A
the pressure produced by the air molecules inside a balloon will first depend on how many air molecules are there, N.  If there weren't any air molecules at all there wouldn't be any pressure.  As you add more and more air to something like a bicycle tire, the pressure increases.  Pressure is directly proportional to N; an increase in N causes an increase in P.  If N doubles, P also doubles (as long as the other variables in the equation don't change).

In B
air pressure inside a balloon also depends on the size of the balloon.  Pressure is inversely proportional to volume, V .  If V were to double, P would drop to 1/2 its original value.

Note
it is possible to keep pressure constant by changing N and V together in just the right kind of way.  This is what happens in Experiment #1 that some students are working on.  Here's a little more detailed look at that experiment.



An air sample is trapped together with some steel wool inside a graduated cylinder.  The cylinder is turned upside down and the open end is stuck into a glass of water sealing off the air sample from the rest of the atmosphere.  This is shown at left above.  Water will move into or out of the cylinder to keep Pout equal to Pin.  We assume that neither of these pressures changes during the experiment.  In this experiment pressure remains constant.

Oxygen in the cylinder reacts with steel wool to form rust.  Oxygen is removed from the air sample which causes N (the total number of air molecules) to decrease.  Removal of oxygen would ordinarily cause a drop in Pin.  But, as oxygen is removed, water rises up into the cylinder decreasing the air sample volume.  N and V both decrease in the same relative amounts and the air sample pressure remains constant.  If you were to remove 20% of the air molecules, V would decrease to 20% of its original value and pressure would stay constant.  It is the change in V that you can measure and use to determine the oxygen percentage concentration in air.



Part C: Increasing the temperature of the gas in a balloon will cause the gas molecules to move more quickly (kind of like "Mexican jumping beans").  They'll collide with the walls of the balloon more frequently and rebound with greater force.  Both will increase the pressure.  You shouldn't throw a can of spray paint into a fire because the temperature will cause the pressure inside the can to increase and the can could explode. 

Surprisingly, as explained in Part D, the pressure does not depend on the mass of the molecules.  Pressure doesn't depend on the composition of the gas.  Gas molecules with a lot of mass will move slowly, the less massive molecules will move more quickly.  They both will collide with the walls of the container with the same force.

The figure below (which replaces the bottom of p. 51 in the photocopied ClassNotes) shows two forms of the ideal gas law.  The top equation is the one we just "derived" and the bottom is a second slightly different version.  You can ignore the constants k and R if you are just trying to understand how a change in one of the variables would affect the pressure.  You only need the constants when you are doing a calculation involving numbers (which we won't be doing).



The ratio N/V is similar to density (mass/volume).  That's where the ρ (density)  term in the second equation comes from.

Here are a couple of examples showing you how you can use the ideal gas law.  These weren't mentioned in class.




A can of spray paint is a sealed rigid container.  That means N (number of gas molecules) and V (volume) stay constant.  Heating up a can of spray paint (something you shouldn't do) will increases the temperature and increase the pressure.  If the pressure gets too high the can will explode.

In this next example we add some air to a tire.

Unless the tire is flat its volume won't change much (we'll assume it doesn't change at all).  We'll assume the temperature of the air is constant also.  But we're adding air so N will increase.  This causes pressure to increase.

Step #2 Charles' Law

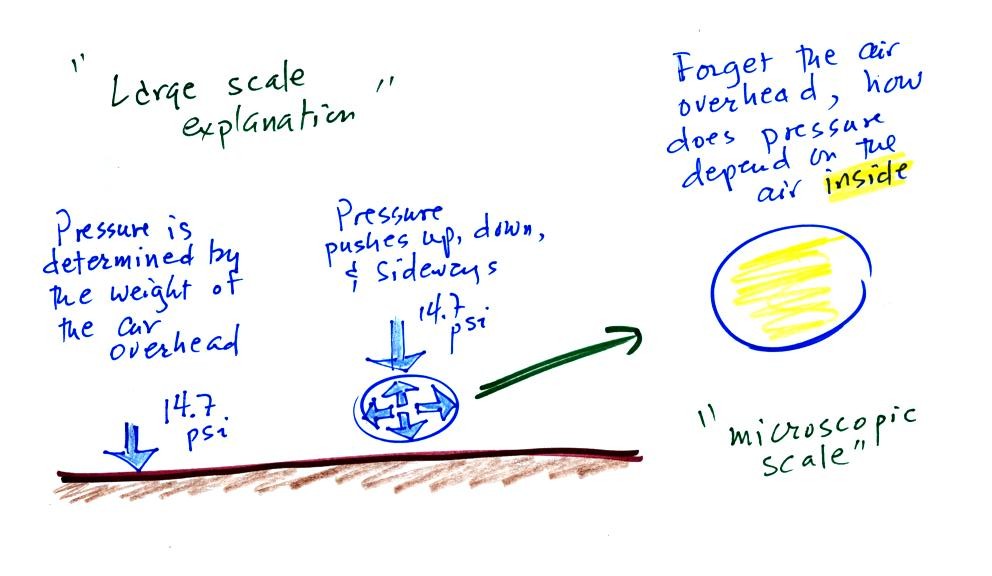
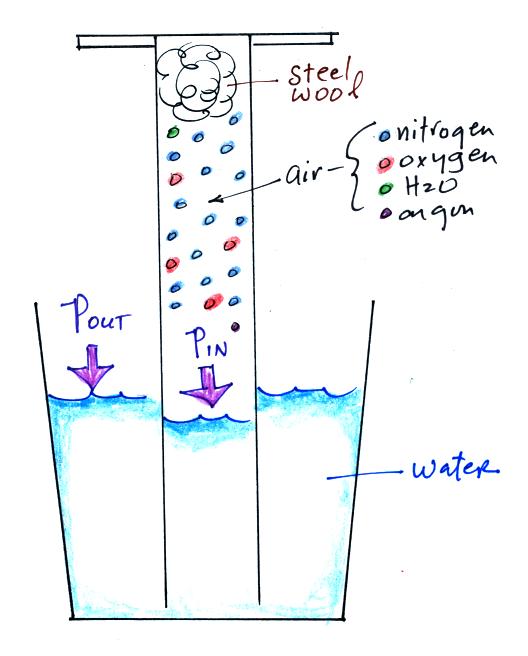
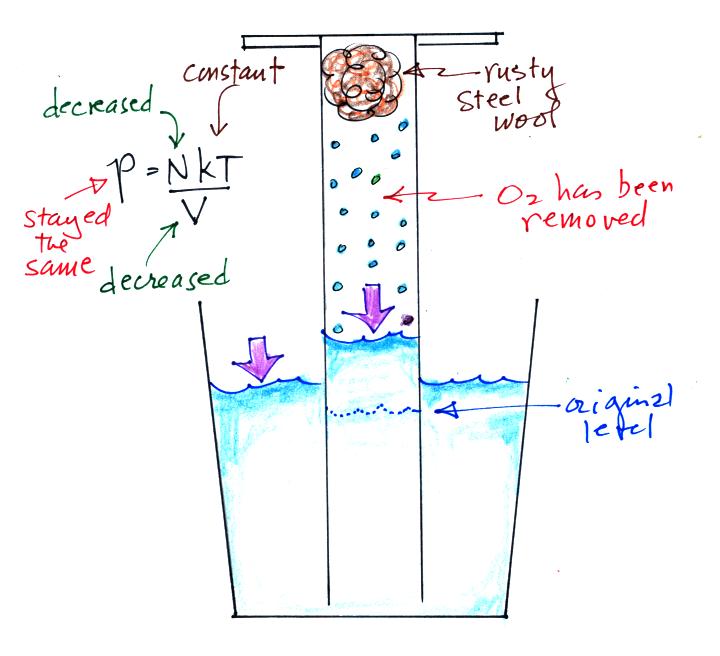
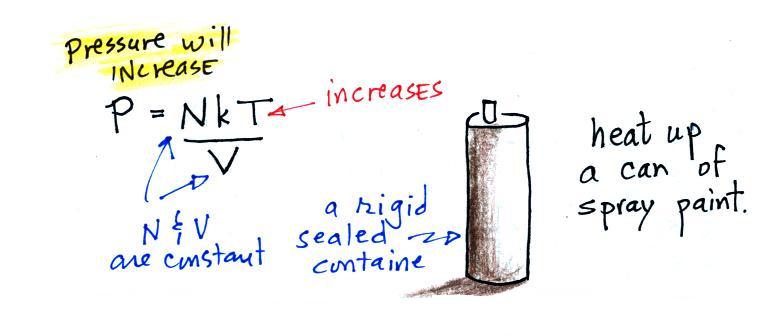
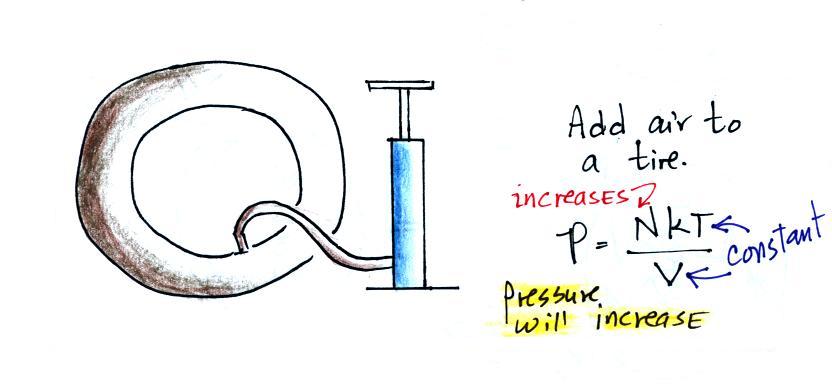
In Charles Law we assume that the pressure of a parcel of air will remain constant (parcel is just another word for volume).  Changing the temperature of a volume of air will cause a change in density and volume and pressure will stay constant.  This is an important situation because this is how volumes of air in the atmosphere behave.

The explanation below is a little more detailed version of what was done in class.

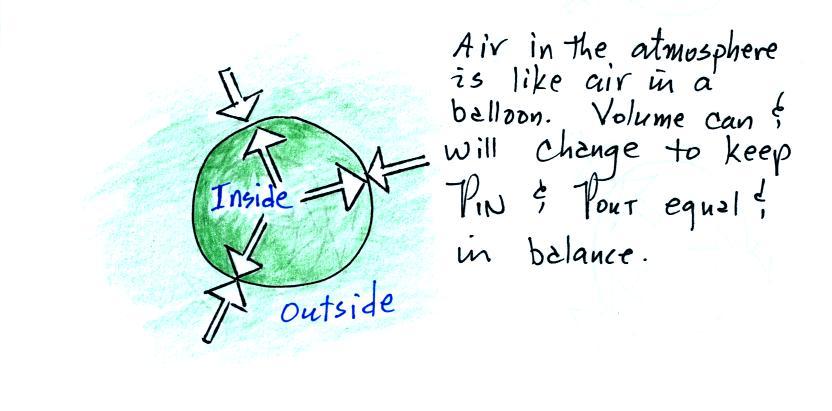
We start with a balloon of air.  The air inside and outside the balloon (or parcel) are exactly the same. 

Note the pressure pushing inward is balanced by the pressure of the air inside the balloon that is pushing outward.  If we change something inside the balloon that upsets this pressure balance, the balloon would expand or shrink until the pressures were again in balance.

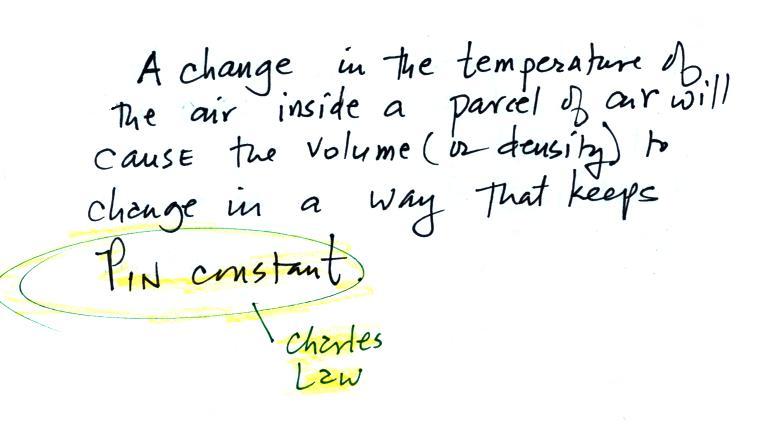
Volumes of air in the atmosphere will always try to keep the pressure of the air inside the parcel constant (P inside is always trying to stay equal to P outside).  That's why we say air in the atmosphere obeys Charles' Law.

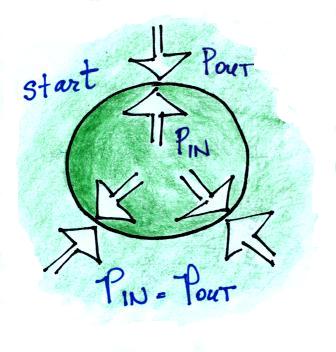
First let's imagine warming the air inside a balloon.  We'll won't change the temperature of the air outside the balloon.




Increasing the temperature will momentarily increase the pressure.  This creates an imbalance.  Now that P inside is greater than P outside the balloon will expand.


Increasing the volume causes the pressure to start to decrease.  The balloon will keep expanding until P inside is back in balance with P outside. 

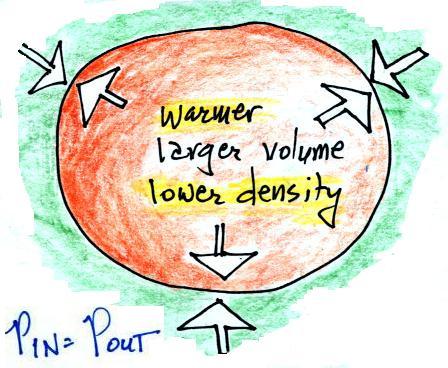
We're left with a balloon that is larger, warmer, and filled with lower density air than it was originally. 





The pressures inside and outside are again the same.  The pressure inside is back to what it was before we warmed the air in the balloon.  You can increase the temperature and volume of a parcel together in a way that keeps pressure constant (which is what Charles' law requires).  Or you can increase the temperature and decrease the density together and keep the pressure constant.l

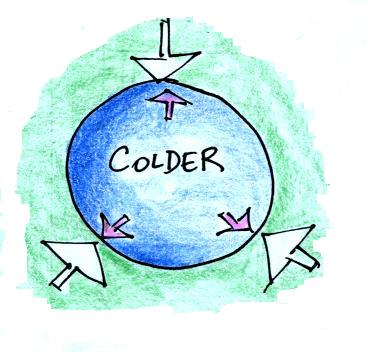
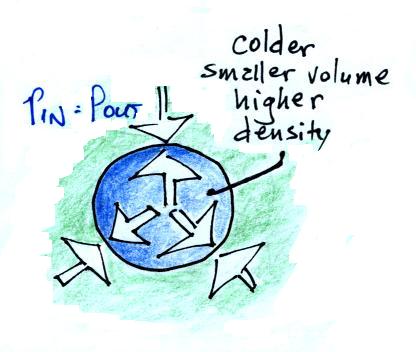
We can go through the same kind of reasoning and see what happens if we cool the air in a parcel.  I've included all the steps below; that wasn't done in class.


We'll start with a parcel of air that has the same temperature and density as the air around it.

We'll cool the air inside the parcel.  The air outside stays the same.

Reducing the air temperature causes the pressure of the air inside the balloon to decrease.  Because the outside air pressure is greater than the pressure inside the balloon the parcel is compressed.


The balloon will get smaller and smaller (and the pressure inside will get bigger and bigger) until the pressures inside and outside the balloon are again equal.  The pressure inside is back to the value it had before you cooled the air in the parcel.


If you want to skip all the details and just remember one thing, here's what I'd recommend (a statement that I didn't show in class)



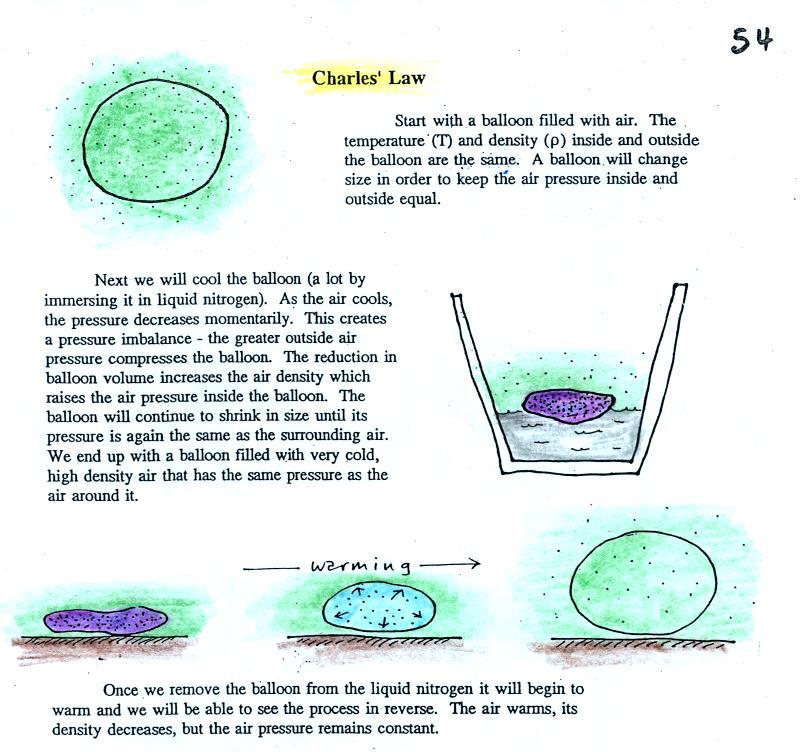
Charles Law can be demonstrated by dipping a balloon in liquid nitrogen.  You'll find an explanation on the top of p. 54 in the photocopied ClassNotes.


The balloon shrinks down to practically nothing when dunked in the liquid nitrogen.  It is filled with very cold, very high density air.  When the balloon is pulled from the liquid nitrogen and starts to warm up it expands.  Density in the balloon decreases.  The volume and temperature keep changing in a way that kept pressure constant (pressure inside the balloon is staying equal to the air pressure outside the balloon).  Eventually the balloon ends up back at room temperature (unless it pops while warming up).

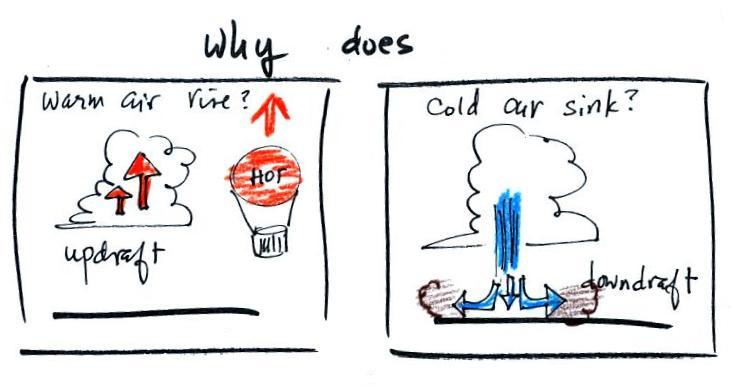
Step #3 Vertical forces acting on parcels of air

And finally the last step toward understanding why warm air rises and cold air sinks.  We'll have a look at the forces that act on parcels of air in the atmosphere.  This information is found on p. 53 in the photocopied ClassNotes.



Basically it comes down to this - there are two forces acting on a parcel of air in the atmosphere.  They are shown on the left hand side of the figure above.

First is gravity, it pulls downward.  The strength of the gravity force (the weight of the air in the parcel) depends on the mass of the air inside the parcel. 

Second there is an upward pointing pressure difference force.  This force is caused by the air outside (surrounding) the parcel.  Pressure decreases with increasing altitude.  The pressure of the air at the bottom of a parcel pushing upward is slightly stronger than the pressure of the air at the top of the balloon that is pushing downward.  The overall effect is an upward pointing force.

When the air inside a parcel is exactly the same as the air outside, the two forces are equal in strength and cancel out.  The parcel is neutrally bouyant and it wouldn't rise or sink, it would just sit in place.

Now have a look at the right hand side of the figure.
If you replace the air inside the balloon with warm low density air, it won't weigh as much.  The gravity force is weaker.  The upward pressure difference force doesn't change (because it is determined by the air outside the balloon which hasn't changed) and ends up stronger than the gravity force.  The balloon will rise.

Conversely if the air inside is cold high density air, it weighs more.  Gravity is stronger than the upward pressure difference force and the balloon sinks.

It all comes down to how the density of the in parcel compares to the density of the air surrounding the parcel.  If the parcel is filled with low density air it will rise.  A parcel full of high density air will sink.

We did a short demonstration to show how density can determine whether an object or a parcel of air will rise or sink.  We used balloons filled with helium (see bottom of p. 54 in the photocopied Class Notes).  Helium is less dense than air even when it has the same temperature as the surrounding air.  A helium-filled balloon doesn't need to warmed up in order to rise.



We dunked the helium-filled balloon in some liquid nitrogen to cool it and to cause the density of the helium to increase.  When removed from the liquid nitrogen the balloon didn't rise, the gas inside was denser than the surrounding air (the purple and blue balloons in the figure above).  As the balloon warms and expands its density decreases.  The balloon at some point has the same density as the air around it (green above) and is neutrally bouyant (it's still cooler than the surrounding air).  Eventually the balloon becomes less dense that the surrounding air (yellow) and floats up to the ceiling (which in ILC 150 is about 30 feet high)

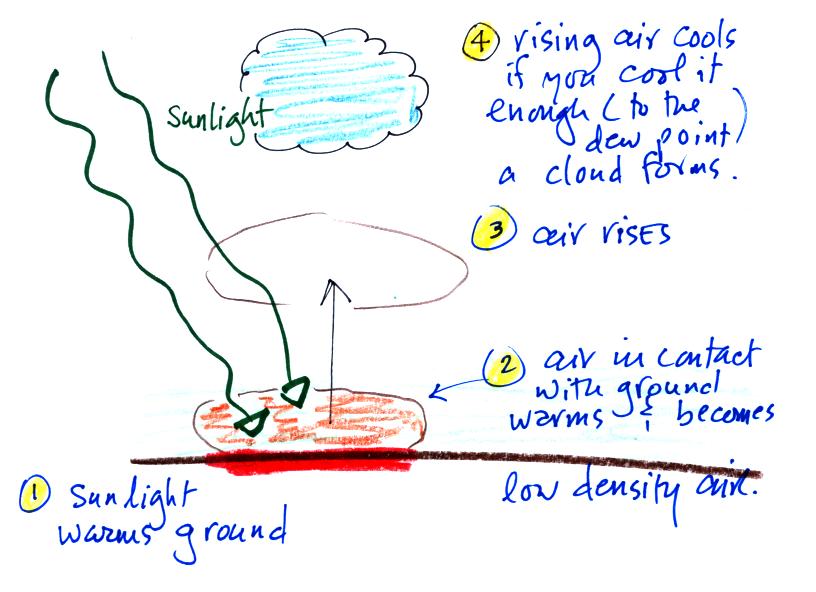
Something like this happens in the atmosphere.  I didn't show the following picture in class.


Sunlight shines through the atmosphere.  Once it reaches the ground at (1) it is absorbed and warms the ground.  This in turns warms air in contact with the ground (2)  As this air warms, its density starts to decrease.  When the air density is low enough, small "blobs" of air separate from the air layer at the ground and begin to rise, these are called "thermals."  (3) Rising air expands and cools (we've haven't covered this yet and it might sound a little contradictory).  If it cools enough (to the dew point) a cloud will become visible as shown at Point 4.  This whole process is called free convection; many of our summer thunderstorms start this way.