Wednesday Oct. 17, 2012
click here to download today's notes in a more
printer friendly format
A song I heard earlier this week while eating lunch, "Somebody That I Used
to Know" from Gotye.
Most of the Experiment #2 reports have been graded and were
returned in class today. You can revise the reports if you want
to (it isn't required). Revised reports are due by Wed., Oct.
31. I should have several reports that were turned in Monday this
week graded in time to return on Friday.
I am also planning on handing out midterm grade summaries in class on
Friday.
The Causes of the Seasons and Ozone and the Ozone Hole 1S1P
reports were collected today. The 3rd Assignment #2 topic is due
next Wednesday.
And here is something I didn't
announce in class, a hidden
optional assignment. Download the assignment if you like and
turn it in on Friday if you'd like to earn some extra credit.
I'll also have another, take home, assignment that I will hand out in
class on Friday. The second assignment will be due at the start
of class next Wednesday (Oct. 24).
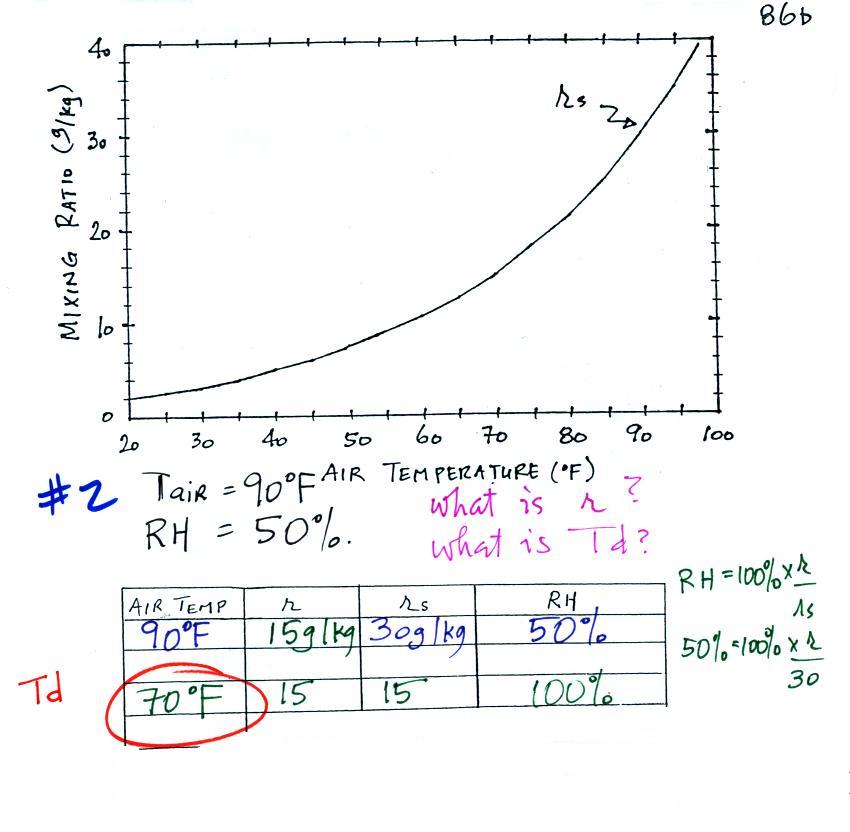
The main event today was working through four humidity
problems. Hopefully this will increase your understanding of the
roles the various humidity variables play and what can cause their
values to change.
Example #1
I gave my notes from class to a student so I'm using
notes from a previous class.
But the notes from class are too hard to sort out even if you were in
class. So
we'll work through this problem in a more detailed, step-by-step manner.
We're given an air temperature of 90 F and a mixing ratio
(r) of 6
g/kg.
We're supposed to find the relative humidity (RH) and
the dew point temperature. We start by entering this
data in the
table.
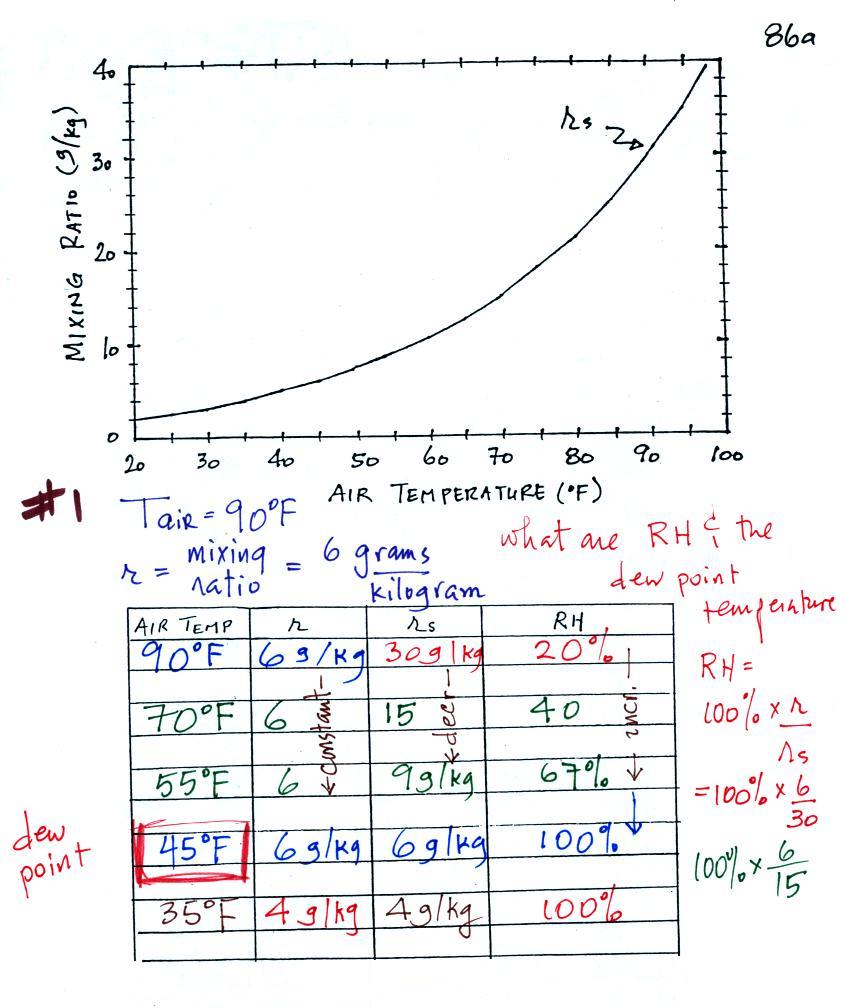
Anytime you know the air's temperature you can look up the
saturation mixing
ratio value on a chart (such as the one on p. 86 in the ClassNotes);
the saturation mixing ratio is 30 g/kg
for 90 F air. 90 F air could
potentially hold 30 grams of water vapor per kilogram of dry air (it
actually contains 6 grams per kilogram in this example).
Once you know mixing ratio and saturation mixing ratio you can
calculate the relative humidity (you divide the mixing ratio by the
saturation mixing ratio, 6/30, and multiply the result by 100%).
You ought to be able to work out the ratio 6/30 in your head (6/30 =
1/5 = 0.2). The RH is 20%.
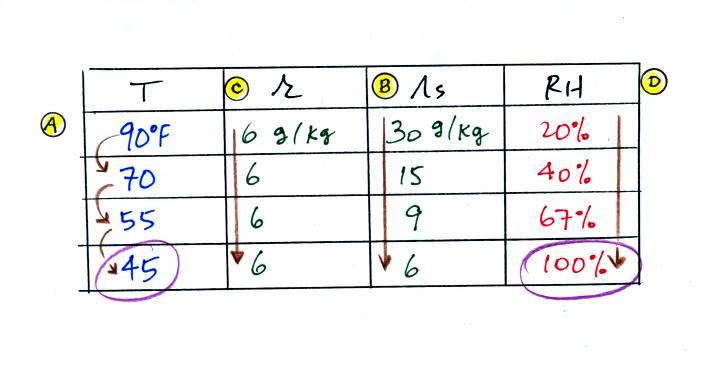
The numbers we just figured out are shown on the top line
above.
(A) We imagined cooling the air from 90F to 70F, then to 55F, and
finally to 45F.
(B) At each step we looked up the saturation mixing ratio and entered
it on the chart. Note that the saturation mixing ratio values
decrease as the air is
cooling.
(C) The mixing
ratio (r) doesn't
change as we cool the air. The only
thing that changes r is adding or removing water vapor and we aren't
doing either. This is probably the most difficult concept to
grasp.
(D) Note how the relative humidity is increasing as we cool
the
air. The air still contains the same amount of water
vapor it is
just that the air's capacity is decreasing.
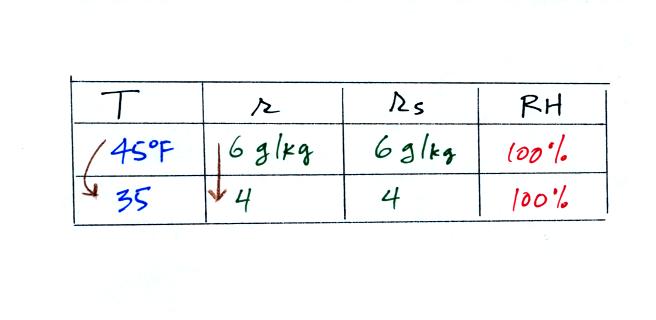
Finally at 45 F the RH becomes 100%. This is kind of a special
point. You have cooled the air until it has become
saturated.
The dew point temperature in
this problem is 45 F.
What would happen if we cooled the air
further still, below the dew
point temperature?
35 F air can't hold the 6 grams of water vapor
that 45 F air can. You can only "fit" 4 grams of water vapor into
the 35 F air. The remaining 2 grams would condense. If
this happened at ground level the ground would get wet with dew.
If it happens above the ground, the water vapor condenses onto small
particles in the air and forms fog or a cloud. Because water
vapor is being taken out of the air (the water vapor is turning into
water), the
mixing
ratio will decrease from 6 g/kg to 4 g/kg. As you cool air below
the dew
point, the RH stays constant at 100% and the mixing ratio decreases.
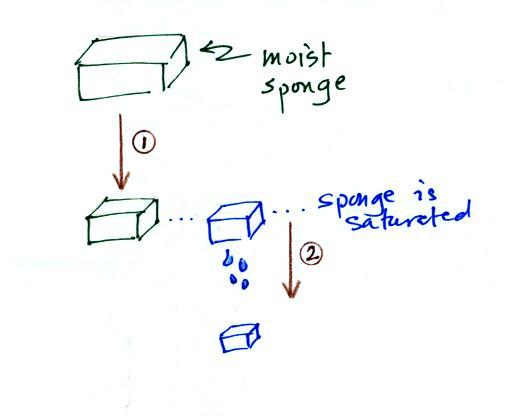
In many ways cooling moist air is liking squeezing a
moist sponge (this
figure
wasn't
shown
in
class)
Squeezing the
sponge and reducing its volume is like cooling moist air and reducing
the saturation mixing ratio. At first (Path 1 in the figure) when
you sqeeze the sponge
nothing happens, no water drips out. Eventually you get to a
point where the sponge is saturated. This is like reaching the
dew point. If you squeeze the sponge any further (Path 2) water
will begin to drip out of the sponge (water vapor
will condense from the air).
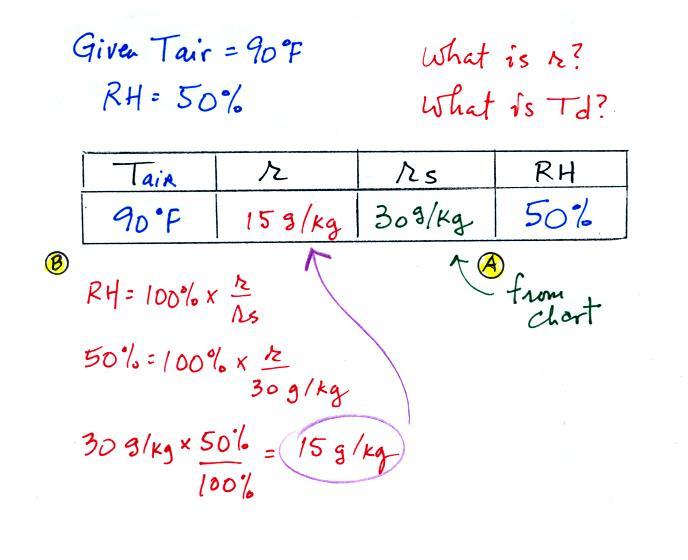
Example 2
We're given an air
temperature
of 90
F and a relative humidity of 50%; we'll try to figure out the
mixing ratio and the dew point temperature. Here's something like
what we ended up with in class.
The
problem is worked out in detail below:
First you fill in the air temperature and the RH data that
you are
given.
(A) since you know the air's temperature you can look up the
saturation mixing ratio (30 g/kg).
(B) Then you might be able to figure out the mixing ratio in your
head. Air that is filled to 50% of its capacity could hold up to
30 g/kg. Half of 30 is 15, that is the mixing ratio. Or you
can substitute into
the relative humidity formula and solve for the mixing ratio. The
details of that calculation are shown above at B.
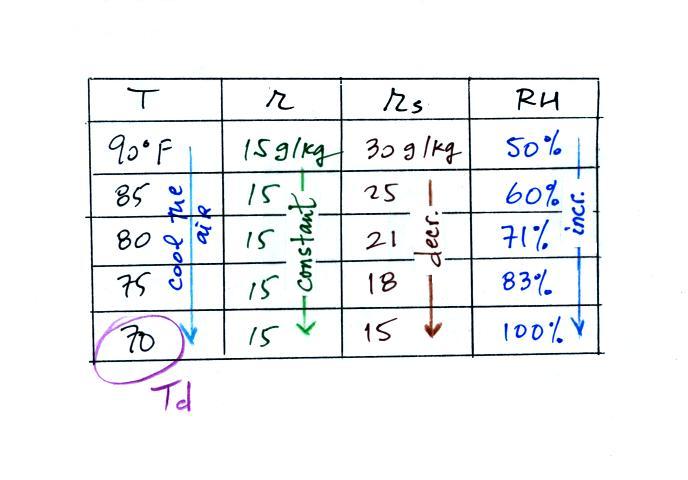
Finally you imagine cooling the air. The
saturation mixing ratio decreases, the mixing ratio stays constant,
and the relative humidity increases. In this example the RH
reached 100% when the air had cooled to 70 F. That is the dew
point temperature.
We can use
results from humidity problems #1 and #2 to
learn and understand a useful rule.
In the first
example the difference between the air and dew point
temperatures was large (45 F) and the RH was low (20%).
In
the
2nd
problem
the
difference
between
the
air
and
dew
point
temperatures
was
smaller
(20
F)
and
the
RH was higher (50%). The easiest way to
remember
this
rule is to remember the case where there is no difference between the
air and dew
point temperatures. The RH then would be 100%.
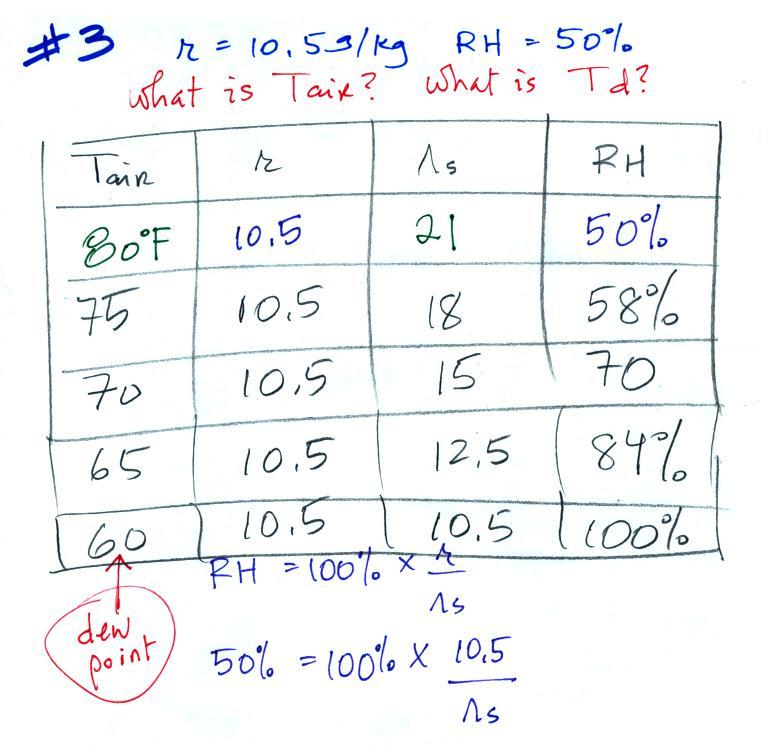
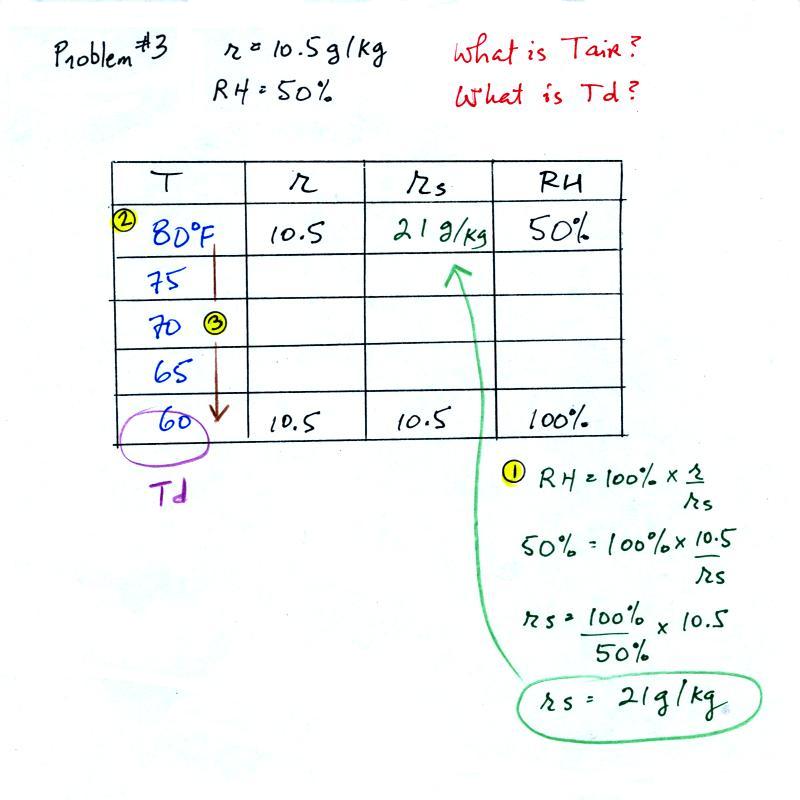
Example 3
You're given the the mixing ratio = 10.5 g/kg and the relative humidity
= 50%. You need to figure
out the air temperature and the dew point temperature.
Here's the play by
play solution to the question
(1) The air contains 10.5 g/kg of water vapor, this is
50%,
half, of what the air
could potentially hold. So the air's capacity, the saturation
mixing ratio must be 21 g/kg (you can either do this in your head or
use the RH equation following the steps shown above).
(2) Once you know the saturation mixing
ratio you can look up the air temperature in a table (80 F air has a
saturation mixing ratio of 21 g/kg)
(3) Then you
imagine cooling the air until the RH becomes 100%. This occurs at
60 F. The dew point is 60 F.
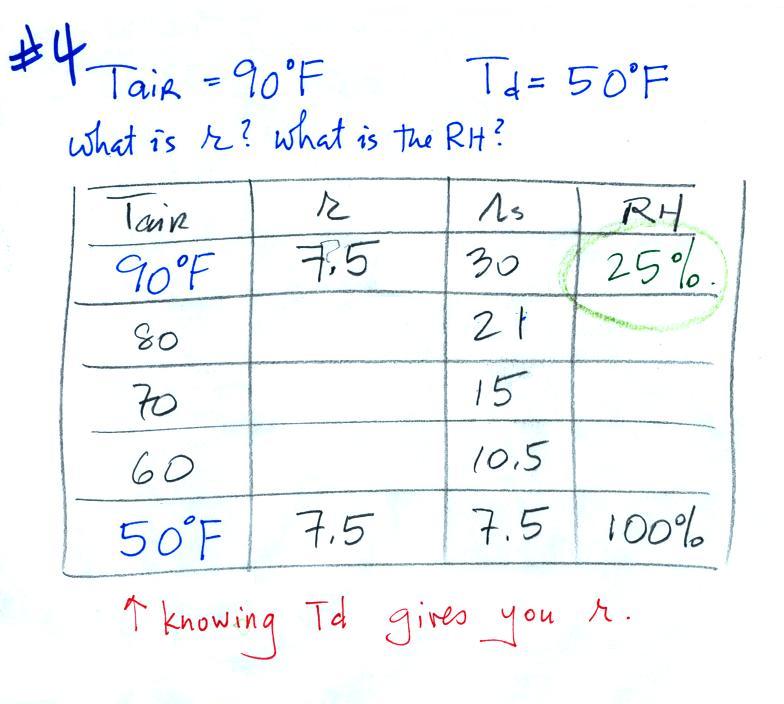
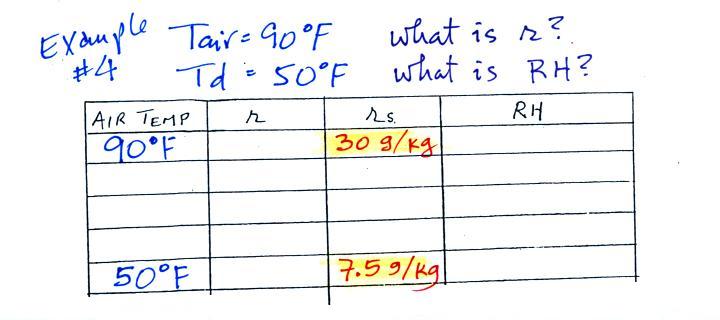
Example 4
Probably the most difficult problem of the bunch.
But one of the
things we said about dew point is that it has the same job as mixing
ratio - it gives you an idea of the actual amount of water vapor in the
air. This problem will show that if you know the dew point, you
can quickly figure out the mixing ratio. Knowing the dew point is
equivalent to knowing the mixing ratio.
Here's what we ended up with in class, we
were given the air temperature and the dew point temperature. We
were supposed to figure out the mixing ratio and the relative
humidity.
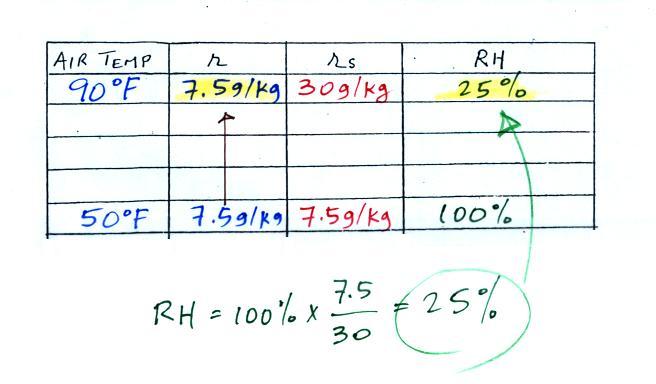
We enter the two temperatures onto a chart and look up the
saturation
mixing ratio for each.
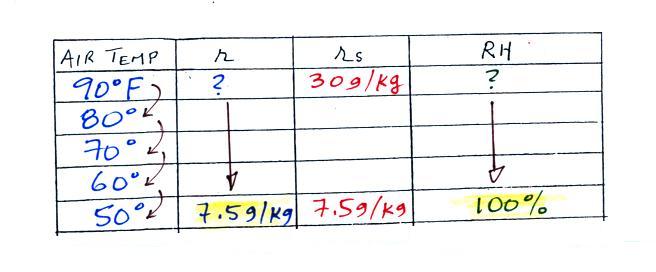
We ignore the fact that we don't know the mixing
ratio. We do know that if we cool the 90 F air to 50 F the RH
will
become
100%. We can set the mixing ratio equal to the value of the
saturation mixing ratio at 50 F, 7.5 g/kg.
Remember back to the three earlier examples. When we
cooled air
to the the dew point, the mixing ratio didn't change. So the
mixing ratio must have been 7.5 all along. Once we know the
mixing ratio in the 90 F air it is a simple matter to calculate the
relative humidity, 25%.
Finally in the last 5 minutes or so I showed a short student made
video tape that described Experiment #3. The object of the
experiment is to measure the energy in sunlight arriving at the ground
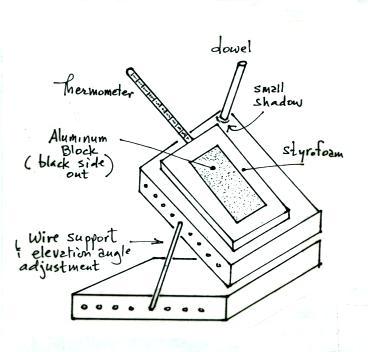
here in Tucson. The apparatus used is sketched below:
It consists of two pieces of wood connected together with a
hinge. A styrofoam insert fits into one of the pieces of wood and
hold a small rectangular piece of metal painted black so that it will
absorb sunlight. There is a hole drilled into the side of the
metal block so that a thermometer can be inserted to measure the
temperature of the block. The block can be elevated and turned so
that it is pointing straight at the sun (rays of sunlight strike the
metal block perpendicularly). When the block is oriented corectly
a small dowel sticking out the front of the apparatus won't cast a
shadow.
A couple of photographs of the apparatus are shown above. You can
see the black metal block, the dowel, and the small piece of wire that
keeps one of the pieces of wood elevated so that it points at the sun.
In the left photo the apparatus hasn't yet been properly oriented and
the dowel is casting a shadow. At right the apparatus has been
turned until the dowel isn't casting a shadow.
After setting up the device you simply the measure the block's
temperature and time while the block heats up. This change of
temperature with time data together with the mass, crossectional area
of the block and the specific heat of aluminum are enough to estimate
the amount of energy striking the block. Click on this link if you would
like to read more about how that is done.